日本大百科全書(ニッポニカ) 「方べきの定理」の意味・わかりやすい解説
方べきの定理
ほうべきのていり
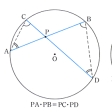
一つの円とその円周上にない1点が与えられていて、その点を通って円と交わる任意の直線を引くとき、直線と円との交点とその点とでできる二つの線分を二辺とする長方形の面積は一定である。これを方べきの定理という。初めの1点をPとし、点Pを通る直線と円との交点をA、Bとすると、PA・PBは点Pを通る直線をどうとっても一定であることを示し、この積を点Pに関するその円の方べきという。点Pを通る直線が円の接線となる場合は、交点A、Bは一致し接点Tとなり、方べきは(PT)2となる。この定理から、円に内接する四角形の場合、二つの対角線についてその交点で分けられる線分の積は等しいことになる。この性質は、四角形が円に内接するための一つの条件でもある。これらの定理は、円周角に関する定理や三角形の相似条件と密接な関係にある。
[柴田敏男]