精選版 日本国語大辞典 「接線」の意味・読み・例文・類語
せっ‐せん【接線・切線】
- 〘 名詞 〙
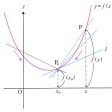
- ① 曲線上の一点でその曲線に接触する直線。曲線C上の点P、Qを結ぶ直線PQが、QをPに限りなく近づけるとき、ある直線lに限りなく近づくならば、この直線lをCの点Pにおける接線という。また、このとき、lはCにPで接するともいう。
- [初出の実例]「微弧に於せざれば、芻亜辟の交角を得ること能はず、切線を知ざれば也」(出典:暦象新書(1798‐1802)下)
- ② 曲面上の一点でその曲線に接触する直線。曲面上の一点Pを通る曲面上の曲線Cに点Pで接する直線lを、その曲面のPにおけるC方向の接線という。また、このとき、lはその曲面にPで接するともいう。
日本大百科全書(ニッポニカ) 「接線」の意味・わかりやすい解説
接線
せっせん
曲線上の点P0と、その近くの点Pとを結んだ直線があり、PをP0に近づけた極限を考えるとき、この直線P0Pが、ある一定の直線lに近づくならば、この直線lを、この曲線上の点P0における接線という。接線は、切線と書いたこともあったが、いまはこの字は使わない。
楕円(だえん)、双曲線、放物線などの二次曲線の曲線上の点P0(x0,y0)における接線の式を
y=m(x-x0)+y0
とすれば、mは、この式を曲線の方程式に代入して得られる二次方程式が重根を有する条件から定められる。関数y=f(x)のグラフ上の点P0(x0,f(x0))における接線の傾きは、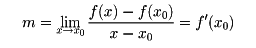
である。したがってf(x)がx=x0で微分可能であることと、曲線y=f(x)が点P0(x0,f(x0))で接線を有することは同値であり、このとき接線の方程式は、
y=f′(x0)(x-x0)+f(x0)
となる。曲線がx=f(t),y=g(t)の形で与えられているとき(空間曲線ならばこれにz=h(t)を加える)、P0(x0,y0)に対応するパラメータの値t0に対して、(dx/dt)t=t0,(dy/dt)t=t0を成分にもつベクトル、すなわち(f′(t0),g′(t0))をこの点における接ベクトルという。接線の方程式は、このとき、uをパラメータとして
x=x0+f′(t0)u, y=y0+g′(t0)u
と表される。
[竹之内脩]
ブリタニカ国際大百科事典 小項目事典 「接線」の意味・わかりやすい解説
接線
せっせん
tangent; tangent line
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
改訂新版 世界大百科事典 「接線」の意味・わかりやすい解説
接線 (せっせん)
tangent
Cを空間における曲線とし,PをC上の1点とする。いま,曲線C上にPと異なる点QをとってPをQに結ぶ直線を考え,Qを曲線Cに沿って限りなくPに近づける。このとき直線PQが限りなく近づく一定の直線が存在するならば,この直線を点Pにおける曲線Cの接線といい,Pをその接点という(図)。Cの各点に接線が存在するとき,これらの接線によって描かれる曲面を曲線Cの接線曲面といい,Cをこの接線曲面の反帰曲線という。Cが一平面上にあるとき,接線もこの平面上にあって,Cが微分可能な関数y=f(x)のグラフであるときには,点P(a,b)におけるCの接線の方程式は,y-b=f′(a)(x-a)となる。なお,この場合,Pにおける接線とx軸との交点をT,Pよりx軸に下ろした垂線の足をMとして,線分PTを接線の長さ,線分TMを接線影という。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「接線」の意味・わかりやすい解説
接線【せっせん】
→関連項目割線|弦(数学)
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の接線の言及
【三角関数】より
…
[三角比]
∠C=90゜の直角三角形ABCにおいて,次の6個の比の値は,角Aの大きさのみで定まり,直角三角形ABCの大きさには無関係である(図1)。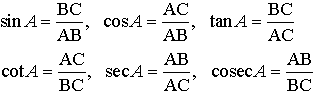 これらの比の値を,それぞれ角Aの正弦(サインsine,記号sin),余弦(コサインcosine,記号cos),正接(タンジェントtangent,記号tan),余接(コタンジェントcotangent,記号cot),正割(セカントsecant,記号sec),余割(コセカントcosecant,記号cosec)といい,これらを総称して三角比という。次に述べる三角関数は三角比の概念の拡張であって,角θが鋭角(0゜<θ<90゜)の場合は上の三角比の定義と一致する。…
これらの比の値を,それぞれ角Aの正弦(サインsine,記号sin),余弦(コサインcosine,記号cos),正接(タンジェントtangent,記号tan),余接(コタンジェントcotangent,記号cot),正割(セカントsecant,記号sec),余割(コセカントcosecant,記号cosec)といい,これらを総称して三角比という。次に述べる三角関数は三角比の概念の拡張であって,角θが鋭角(0゜<θ<90゜)の場合は上の三角比の定義と一致する。…
【円】より
…したがって,同じ弧の上の円周角はすべて等しく,共役な弧の上の円周角の和は180度である。
[接線と割線]
lを円の載っている平面上の直線とする。円の中心Oからlまでの距離が半径より大きければlは円に交わらず,その距離が半径より小さければlは円周と2点で交わる。…
※「接線」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...