円周角（読み）エンシュウカク

デジタル大辞泉

えんしゅう‐かく〔ヱンシウ‐〕【円周角】

円周上の一点から他の二点に引いた二つの弦のつくる角。

出典　小学館

精選版 日本国語大辞典

えんしゅう‐かくヱンシウ‥【円周角】

1. 〘 名詞 〙 円周上の一点から、同一円周上の他の二点に引いた二個の弦によってできる角。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

円周角
えんしゅうかく

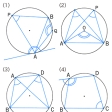
円周上の3点をA、B、Pとするとき、角APBをこの角内にある弧(こ)ABに対する円周角、あるいは、弧ABの上に立つ円周角という（図の(1)）。円の中心をOとすると、この弧ABに対する中心角AOBは、円周角APBの2倍に等しい（図の(2)）。したがって、共役弧(きょうやくこ)の上の点のとり方にかかわらず、一つの弧に対する円周角の大きさは一定である。劣弧に対する円周角は鋭角、優弧に対する円周角は鈍角である。とくに半円に対する円周角は直角である。一つの線分を見込む角が一定な点の全体は、その線分を弦(げん)とする円の弧となり、線分の両側にできる。円の接線とその接点を一端とする弦とのなす角は、その角の内部にある弧に対する円周角と等しい。

　四角形の四つの頂点が一つの円周上にあるとき、その四角形は円に内接するといい、その円を四角形の外接円という。四角形ABCDが円に内接するとき、円周角の性質から∠BAC＝∠BDCである（図の(3)）。この逆も成り立つ。すなわち、上記二つの角が等しければ、この四角形は円に内接する。また、円に内接する四角形の対角の和は2直角である（図の(4)）。この逆も成り立つ。さらに、円に内接する四角形の一つの外角は、その頂点に対する角（内対角という）と等しい。この性質も四角形が円に内接する条件である。

［柴田敏男］

円周角〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

円周角 (えんしゅうかく)

→円（数学）

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の円周角の言及

【円】より

…前者を劣弧といい，後者を優弧という。弧ABの共役弧の上に点Pをとり，∠APBを弧ABの上の円周角という(図2)。弧ABの上の円周角∠APBは，その弧の中心角∠AOBの半分である。…

※「円周角」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」