対角線（読み）タイカクセン

デジタル大辞泉

たいかく‐せん【対角線】

多角形で、隣り合わない二つの頂点を結ぶ線分。また多面体で、同一平面上にない二つの頂点を結ぶ線分。
[類語]線・ライン・筋すじ・弧・罫・線条・直線・曲線・実線・破線・点線・波線・斜線・アンダーライン・傍線・折れ線・垂線・鉛直線・接線・水平線・平行線・双曲線・放物線・母線・螺線らせん・割線・中線・中心線

出典　小学館

精選版 日本国語大辞典

たいかく‐せん【対角線】

1. 〘 名詞 〙
2. ① 多角形で、同一の辺上にない二つの頂点を結んで得られる線分。また、多面体で、同一の面上にない二つの頂点を結んで得られる線分。〔改正増補物理階梯（1876）〕
3. ② 比喩的に、①に当たる経路や、それを通って移動するさまなどをいう。
   1. [初出の実例]「をばさまのこの『寮』(ヴィラ)から、町を対角線に抜けて」(出典：唐人お吉（1928）〈十一谷義三郎〉一)

対角線の語誌

中国の明末に、ユークリッドの原著をマテオ=リッチが口訳し徐光啓が漢訳した「幾何原本」（一六〇七）に「凡平行線方形、若於両対角作_二一直線_一、其直線為_二対角線_一」とある。近世、この書は日本の数学者にも読まれて、幕末明治初期に西洋数学を導入する過程で採用されて、一般化した。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

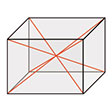
対角線 (たいかくせん)
diagonal

多角形において，相隣らない2頂点を結ぶ線分を対角線という。n角形はn（n－3）/2個の対角線をもつ。凸多角形では対角線はみな多角形の内部にあるが，凹多角形ではそうとは限らない。凹多角形の対角線を内部にあるものだけに限定することもある。n角形はその内部にある適当なn－3個の対角線によってn－2個の三角形に分割される。多面体において，同一の面に含まれない2頂点を結ぶ線分を多面体の対角線という。
執筆者：中岡 稔

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

対角線
たいかくせん
diagonal

(1) 多角形では，隣合わない2つの頂点を結ぶ線分をいう。 n 角形の対角線の個数は n(n－3)/2 である。 (2) 多面体では同一の面に属しない2つの頂点を結ぶ線分をいう。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

対角線【たいかくせん】

多角形では，隣合わない二つの頂点を結ぶ線分。多面体では，同一平面上にない２頂点を結ぶ線分。

出典　株式会社平凡社

世界大百科事典（旧版）内の対角線の言及

【行列】より

…　Aが正則なのは，c_n≠0のときで，このとき，　A^－1＝－c_n^－1(A^n－1＋c₁A^n－2＋……＋c_n－2A　　＋c_n－1I)であるから，上の結果は逆行列の計算にも利用できる。　正方行列においては，(i,i)成分の位置を総称して対角線という。対角線以外の場所の成分が全部0の正方行列を対角型の行列という。…

【四辺形】より

…四辺形ABCDにおいて，∠Aと∠C，∠Bと∠Dを対角といい，辺ABと辺CD，辺BCと辺DAを対辺という。また，線分AC,BDを対角線という。凸四辺形では対角線は四辺形の内部にあるが，凹四辺形ではそうとは限らない。…

※「対角線」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」