事象（読み）ジショウ

デジタル大辞泉

じ‐しょう〔‐シヤウ〕【事象】

１ ある事情のもとで、表面に現れた事柄。現実の出来事。現象。「自然界の事象」
２ 数学で、試行の結果起こる事柄。例えば、さいころを投げるという試行の結果からは一から六の目のどれかが出るという事象が起こる。
[類語]事・事物・物事・現象・出来事・余事・余所よそ事・他事・他人事・人事ひとごと・雑事・諸事・事件・時事・事柄・事故・異変・大変・急変・変事・大事だいじ・大事おおごと・小事・細事・些事・世事・俗事・私事しじ・私事わたくしごと・用事・珍事・不祥事・アクシデント・ハプニング・センセーション

出典　小学館

精選版 日本国語大辞典

じ‐しょう‥シャウ【事象】

1. 〘 名詞 〙
2. ① いろいろの物事や現象。
   1. [初出の実例]「その詩と想と体と所詠の事象と」(出典：比興詩を論ず（1905）〈角田浩々歌客〉六)
3. ② 数学で、試行の結果起こる事柄。たとえば、賽(さい)を振るという試行に対しては、一の目が出る、偶数の目が出る、四以上の目が出る、などの事象が考えられる。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

事象 (じしょう)
event

数学用語。偶然現象において，起こりうるそれぞれの可能性に対して確率を対応させようとするとき，その対象となる事柄が事象である。数学的には次のように記述される。例えばさいを投げる場合，それぞれの目が出るのはいろいろな偶然に支配される結果と考え，それら偶然をパラメーターωで表す。1の目が出たのはω₁が支配した結果，2の目はω₂が，……，6の目はω₆が支配したものと考える。これらωを根元事象と呼び，根元事象の集合を事象という。正しいさいなら各ωに1/6の確率を与えることになる。偶数の目がでる事象は集合｛ω₂，ω₄，ω₆｝であり，その確率は各根元事象の確率の和3×1/6＝1/2である。起こりうる可能性が無限個ある場合でも，それが可算個であれば，根元事象ω₁，ω₂，……，ω_n，……を考え，さいの場合と同様にそれらの集合としての事象やその確率を決めることができる。しかし，測定値の誤差のように偶然の値が連続量となる場合，数学的記述は複雑になる。パラメーターωの全体（それは非可算無限集合）をΩとし，Ωの部分集合の族で次の条件を満たすものをBとかく。（1）Ω∈B，（2）A₁，A₂，……，A_n，……がすべてBの要素なら和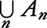もBに属する，（3）A∈BならばA^c＝Ω－A∈B。このときBの要素を事象といい，事象A^cをAの余事象と呼ぶ。また，二つの事象A，Bの共通集合が空であるときに，両者は排反（排反事象）であるという。事象Aに確率P（A）を与えて確率空間（Ω，B，P）が得られる。それはP（Ω）＝1である測度空間にほかならない。このような空間のうえでは無限個の事象や極限なども含め複雑な偶然現象を数学的に厳密に扱うことができる。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

事象【じしょう】

確率の用語。ある試行または観察（たとえば，さいころを10回振る）を行った結果起こり得るいろいろな場合のうち，ある条件（たとえば１の目が３回出る）に当てはまるもの。→従属事象／独立事象／排反事象
→関連項目大数の法則

出典　株式会社平凡社

普及版 字通

【事象】じしよう

事況。

字通「事」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の事象の言及

【確率】より

…次いで18世紀に入り，ヤコブ･ベルヌーイの遺稿が，甥のニコラウスによってまとめられ，《推測法》(1713)として出版されたが，そこには順列，組合せを用いた確率の話が出てきて，しだいに確率論としての形態を整えてきたのであった。　ここでも創生期のように有限個の事象を扱った確率から話を始める。例えば，銅貨を投げるとき，それがゆがんでいないなら表の出る確率と裏が出る確率が同じであるとしてよかろう。…

※「事象」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」