等長変換（読み）とうちょうへんかん

日本大百科全書(ニッポニカ)

等長変換
とうちょうへんかん

一つの距離空間を自分自身に写す写像で、任意の2点間の距離を変えないものを等長変換という。したがって、平面や空間の等長変換は合同変換にほかならない。以下、さらに等長変換の例をあげるため、空間のいろいろな部分集合Sを距離空間として考えるが、Sの点と点の間の距離として、この2点を結ぶS内の最短経路の長さをとるものとする。球面の中心を通る任意の直線の周りの回転移動はこの球面の等長変換である。もっと一般に、ある直線の周りの回転移動は、この直線を軸とする回転体の等長変換となる。また、楕円(だえん)面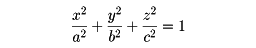

において、xy、yz、zx平面に関する対称移動はいずれも等長変換である。しかし、これらの距離空間をすこし歪(ゆが)めてみればわかるように、一般の距離空間には等長変換は恒等写像しかない。また、等長変換を多くもつ距離ほどいい形をしているといえる。

［高木亮一］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

等長変換
とうちょうへんかん
isometry

一般に，距離空間で距離を不変とする変換を等長変換という。ユークリッド空間の等長変換は合同変換である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の等長変換の言及

【ユニタリ変換】より

…　内積の定義された複素ベクトル空間の概念を無限次元に拡張したものがヒルベルト空間である。ヒルベルト空間Hにおける一次変換Uでベクトルの長さを不変にするものを等長変換というが，無限次元の場合は等長変換がHをH全体に写すとは限らない。ヒルベルト空間HをH全体に写す等長変換を，ユニタリ変換，またはユニタリ作用素という。…

※「等長変換」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」