翻訳|ellipse
精選版 日本国語大辞典 「楕円」の意味・読み・例文・類語
だ‐えん‥ヱン【楕円・橢円】
日本大百科全書(ニッポニカ) 「楕円」の意味・わかりやすい解説
楕円
だえん
ellipse
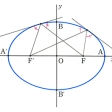
円錐曲線(えんすいきょくせん)の一つ。長円ともいう。2定点F、F′からの距離の和が一定である点の軌跡が楕円であり、F、F′をその焦点という()。F、F′を通る直線をx軸とし、線分FF′の垂直二等分線をy軸とする直交座標系をとれば、楕円は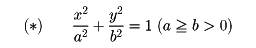
の形の方程式で表される。F、F′が一致すれば円となるので、円は楕円の一種である。Oを楕円の中心、中心を通る弦を直径という。とくにのAA′、BB′をそれぞれ長軸、短軸、これらをあわせて主軸という。一方の焦点から出た光は楕円で反射してすべて他方の焦点に集まる、という性質をもつ。x2+y2=a2なる円を楕円(*)の補助円という()。
x=acos , y=bsin
, y=bsin
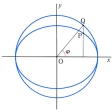
なる点P(x, y)は楕円上にあり、x′=acos , y′=asin
, y′=asin なる点Q(x′, y′)は補助円上にあるから、楕円は補助円をy軸方向にb:aの比で収縮したものである。x軸とQOによってつくられる角
なる点Q(x′, y′)は補助円上にあるから、楕円は補助円をy軸方向にb:aの比で収縮したものである。x軸とQOによってつくられる角 をPの離心角という。一つの直径g1に平行な弦の中点の軌跡はまた一つの直径g2となる。このときg2に平行な弦の中点の軌跡はg1で、g1とg2とは互いに共役な直径といわれる()。
をPの離心角という。一つの直径g1に平行な弦の中点の軌跡はまた一つの直径g2となる。このときg2に平行な弦の中点の軌跡はg1で、g1とg2とは互いに共役な直径といわれる()。
楕円はまた、定直線と定点からの距離の比が1より小さい一定値である点の軌跡、ともいうことができる。にそのような定直線と定点の組l、Fとl′、F′とを書いてある。l、l′を準線という。一定値eは楕円の離心率といわれ、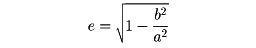
で与えられる。λを径数(パラメーター)とする二次曲線群
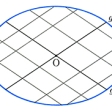
は、λ<βならば楕円を、β<λ<αならば双曲線を表し、すべて同じ焦点〔=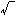 (α-β), 0〕をもつ。このとき、平面上の原点以外の任意の点Pを通って、この二次曲線群の一つの楕円と一つの双曲線があり、それらはPで互いに直交する()。このように焦点を共有する楕円、双曲線は共焦点であるという。
(α-β), 0〕をもつ。このとき、平面上の原点以外の任意の点Pを通って、この二次曲線群の一つの楕円と一つの双曲線があり、それらはPで互いに直交する()。このように焦点を共有する楕円、双曲線は共焦点であるという。
楕円は円錐曲線の一つとして紀元前200年以上前にアポロニウスらによって学問的に研究された。それが2000年近くもたってから「惑星は太陽を一焦点とする楕円軌道を描く」というケプラーの法則によって実用上の意味をもつことになったのは興味深い。
[立花俊一]
改訂新版 世界大百科事典 「楕円」の意味・わかりやすい解説
楕円 (だえん)
ellipse
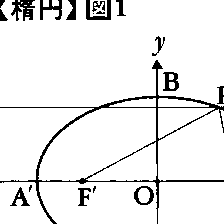
平面上で,2定点F,F′からの距離の和が一定値であるような点によって描かれる図形を楕円,または長円といい,FとF′をその焦点という。1定値を2aとし,線分FF′の長さを2cとするとき,e=c/a(<1)を離心率という。線分FF′の中点を楕円の中心という。直線FF′と,楕円との交点をA,A′とし,中心Oにおいて直線FF′に立てた垂線と楕円との交点をB,B′とするとき,線分AA′は線分BB′より長い。線分AA′を長軸,線分BB′を短軸といい,これらを合わせて主軸という。直線AA′をx軸,直線BB′をy軸にとるとき,上の楕円の方程式は,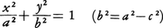
となる。このときx=±a2/cで表される2直線d,d′を準線という(図1)。楕円上の点Pから焦点F(c,0)までの距離と,Pから準線x=a2/cまでの距離の比は一定で離心率eに等しい。焦点F′(-c,0)と準線x=-a2/cについても同様である。楕円の長軸を直径とする円を補助円という。補助円の周上の点Qから長軸に下ろした垂線の足をRとして,線分QRと楕円との交点をPとするとき,QR:PR=a:bである。楕円は媒介変数θを用いて,x=acosθ,y=bsinθの形に表される。このθを楕円上の点P(x,y)の離心角という。楕円への二つの接線が直交するような点は一つの円を描き,その中心は楕円の中心と一致し,半径は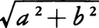 である(図2)。この円を準円という。楕円の周の長さは楕円積分,
である(図2)。この円を準円という。楕円の周の長さは楕円積分,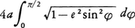
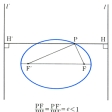
で与えられ,楕円で囲まれた図形の面積はπabである。線分MN上に点Pがあって,MとNが直交する直線上を動くとき,Pは楕円を描く(図3)。空間で直線mをこれと交わる直線lのまわりに回転したときに生ずる曲面を円錐面というが,いまlとmの交点を通らない平面πで,πのlに対する傾きがmのlに対する傾きより大きいものをとり,πで円錐面を切れば,切口は楕円となる。この意味で楕円は円錐曲線の一種である。この場合,πと1点で接し,円錐面と円で接する球面をとれば,πとの接点が楕円の焦点となり,円の平面とπとの交線が準線となる。なお,円を離心率が0である楕円とみなし,楕円の仲間に入れるのがふつうである。
→二次曲線
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「楕円」の意味・わかりやすい解説
楕円
だえん
ellipse
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「楕円」の意味・わかりやすい解説
楕円【だえん】
→関連項目長円
出典 株式会社平凡社百科事典マイペディアについて 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

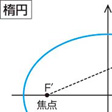

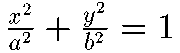 で表わされる。このときx軸上の径の長さは 2a、y軸上の径の長さは 2b で、長い方を長軸、短い方を
で表わされる。このときx軸上の径の長さは 2a、y軸上の径の長さは 2b で、長い方を長軸、短い方を