合同変換（読み）ごうどうへんかん（その他表記）motion
congruent transformation

精選版 日本国語大辞典

ごうどう‐へんかんガフドウヘンクヮン【合同変換】

1. 〘 名詞 〙 ユークリッド空間の二点間の距離を変えない点変換。平行移動、回転移動、折り返し、また、その組合わせ。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

合同変換 (ごうどうへんかん)
motion
congruent transformation

平面上の各点をその平面上の点にうつす写像によって，任意の2点間の距離が不変に保たれるとき，この写像を合同変換，または運動という。平面上の各点を一定の方向に一定の距離だけずらせた点にうつす平行移動（図1），平面上の各点を一定点のまわりに一定角だけ回転した点にうつす回転移動（図2），平面上の各点を一定直線に関して対称な点にうつす折返し（対称移動）（図3）はいずれも平面上の合同変換である。平面上の合同変換によって平面はそれ自身の上に1対1にうつり，図形は位置を変えるだけでその形や大きさを変えない。こういうわけで，合同変換は力学でいう剛体の運動にあたる。二つの合同変換f，gを合成したgf，すなわち点aを点g（f（a））にうつす写像も合同変換である。平面上の合同変換は平行移動と回転移動の合成，またはそれと折返しの合成で表され，平行移動と回転移動は2個の折返しの合成で表される（図4，5）。合同変換の全体は合成を積とすることによって群をつくる。これを合同変換群，または運動群という。平面上に直交座標系をとるとき，合同変換は座標が（x，y）である点を次式で与えられる（x′，y′）を座標にもつ点にうつす写像として解析的に表示される。

　x′＝ax＋by＋e，y′＝cx＋dy＋f

ここにa，b，c，d，e，fは定数であって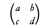，は直交行列，すなわちa²＋b²＝1，c²＋d²＝1，ac＋bd＝0を満たすものとする。

　平面ユークリッド幾何学は，平面上の図形の性質のうち任意の合同変換で不変な性質を研究する幾何学であるということができる。以上では，平面上の合同変換について述べたが，空間の合同変換についても同様のことがいえる。ただし，回転移動，折返しはそれぞれ一定点，一定直線に変えて一定直線，一定平面に関して考えるものとする。
執筆者：中岡 稔

図1～図5

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

合同変換
ごうどうへんかん

平面を自分自身の上へ写す写像で、任意の2点間の距離を変えないものをいう。基本的なものとして、(1)回転移動、(2)平行移動、(3)対称移動、の3種類がある。定点の周りを定角だけ回すのが回転移動であり、定方向に定距離だけ動かすのが平行移動であり、定直線に関して折り返すのが対称移動である。この3種類の移動をいくつか組み合わせたものも、あるいは任意の点を動かさないという写像も合同変換である。

　なお、合同変換で写す限り、任意の図形は形状と大きさを変えない、すなわち、元の図形と合同である。とくに、3点A、B、Cを合同変換で写した点をA'、B'、C'とすれば、△ABCと△A'B'C'は合同になり、初等数学で教える三角形の合同条件
〔1〕AB＝A'B'，BC＝B'C'，CA＝C'A'　　　　　　　　　　（三辺相等）
〔2〕AB＝A'B'，BC＝B'C'，∠ABC＝∠A'B'C'　　　　　　（二辺夾角(きょうかく)相等）
〔3〕AB＝A'B'，∠CAB＝∠C'A'B'，　∠ABC＝∠A'B'C'　（一辺両端角相等）
を満たす。

　空間を空間自身の上へ写す写像で、任意の2点間の距離を変えないものを（空間上の）合同変換といい、(1)平行移動、(2)平面に関する対称移動、(3)直線の周りの回転移動、が基本的である。任意の図形と、それを合同変換した図形が合同になるなどの性質は、平面の場合と同様である。

［高木亮一］

合同変換（回転移動、平行移動、対称移動…

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

合同変換
ごうどうへんかん
congruent transformation

ユークリッド空間における一対一の点対応であって，その任意の2点間の距離が，対応する2点間の距離と等しい点変換を，合同変換という。この変換によって直交座標系は，直交座標系に移される。平行移動，回転，折返し，およびそれらの組合せはすべて合同変換である。また，距離空間における等長変換ということもある。

出典　ブリタニカ国際大百科事典 小項目事典