距離空間（読み）キョリクウカン（その他表記）metric space

デジタル大辞泉

きょり‐くうかん【距離空間】

任意の二点間に距離が定義される空間。例えば、平面上の二点間では距離が定義できるから、平面は距離空間である。

出典　小学館

精選版 日本国語大辞典

きょり‐くうかん【距離空間】

1. 〘 名詞 〙 数学で、距離の定義された集合。集合Ａのどの二元ａ、ｂに対しても、一つの実数 d(a, b) が対応し、次の四つの条件がみたされる場合のＡをいう。d(a, b)≧0、d(a, b)=0 ということと、a=b ということとは同値である。d(a, b)= d(b, a)、d(a, c)≦d(a, b)+d(b, c)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

距離空間 (きょりくうかん)
metric space

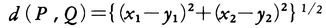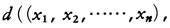
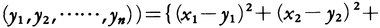
平面上の2点P，Qの距離をd（P，Q）で表したとき，次の3条件が成り立つ。（1）d（P，Q）≧0でかつP＝Qのときに限ってd（P，Q）＝0，（2）d（P，Q）＝d（Q，P），（3）d（P，R）≦d（P，Q）＋d（Q，R）。一般に，集合Sにおいて，その任意の2元P，Qに対して一つの実数d（P，Q）が定められていて，上の3条件が成り立つとき，Sを距離空間といい，d（P，Q）をPとQの距離という。平面上の点P，Qを直交座標により（x₁，x₂），（y₁，y₂）で表すとき，となる。一般に，n個の実数の組（x₁，x₂，……，x_n）全体の集合において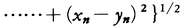と定義すれば距離空間が得られる。これをn次元ユークリッド空間Euclidean spaceという。また閉区間［a，b］で定義された連続関数は，その2元f，gに対して，d（f，g）＝max｛｜f（x）－g（x）｜;a≦x≦b｝と定義すれば距離空間となる。距離空間では開集合などの概念が定義され，距離空間は位相空間となる。
執筆者：中岡 稔

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

距離空間
きょりくうかん
metric space

集合 R の任意の2点 x ，y に対して，1つの正数 ρ(x，y) が，次の性質を満足するように定義できるとき，この集合 R を距離空間という。 (1) ρ(x，x)＝0 ，(2) ρ(x，y)＝0 なら x＝y ，(3) ρ(x，y)＝ρ(y，x) ，(4) ρ(x，y)＋ρ(y，z)≧ρ(x，z) 。 ρ を2点 x ，y の組と ρ(x，y) との対応と考えれば，ρ は1つの関数である。この関数を距離関数といい，実数 ρ(x，y) を x と y の距離という。このような距離の定義されている位相空間を距離空間という。ユークリッド空間 ,ヒルベルト空間，フレッシェの空間などがその例である。

出典　ブリタニカ国際大百科事典 小項目事典