連立二次方程式（読み）れんりつにじほうていしき（英語表記）simultaneous quadratic equation

改訂新版　世界大百科事典

連立二次方程式 (れんりつにじほうていしき)
simultaneous quadratic equation

連立代数方程式f₁（x₁，……，x_n）＝0，……，f_r（x₁，……，x_n）＝0はf₁，……，f_rの次数がすべて二次以下で，少なくとも一つは二次のものがあるとき連立二次方程式と呼ぶ。n＝2，r＝2の場合を考えてみよう。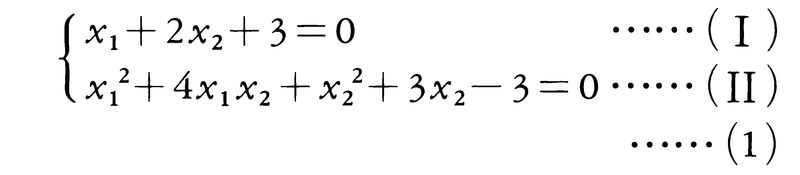

を解いてみると，（Ⅰ）からx₁＝－2x₂－3となるが，これを（Ⅱ）に代入してx₂についての二次方程式を得る。それを解いてx₂＝2，－1がでる。この値を（Ⅰ）に代入して，（x₁，x₂）＝（－7，2），（－1，－1）という解を得る。この例のように一方の方程式が一次ならば，それを使って例えばx₁をx₂で表し，他方の方程式に代入してx₂についての二次方程式を得る。これからx₂が求まり，最初の方程式によりx₁も求まる。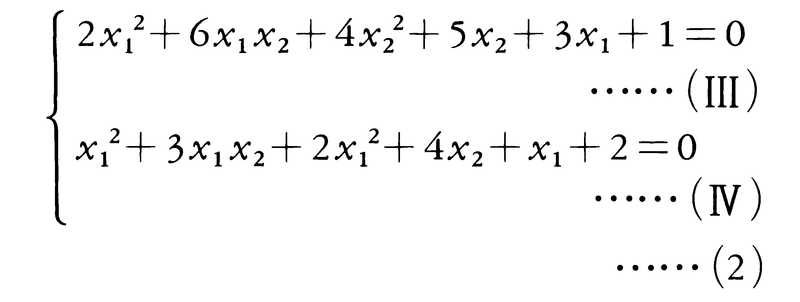

のように一方の二次式の部分が他方の二次式の部分の定数倍ならば，一方の定数倍から他方を引いて一次方程式を得る（上の例の場合（Ⅲ）－2×（Ⅳ））。したがって（1）の場合に帰着する。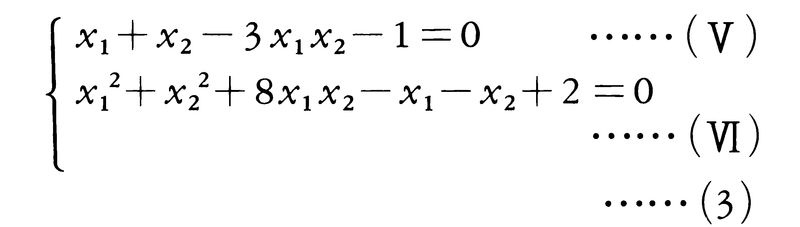

のように，x₁，x₂に関して対称であるとき，u＝x₁＋x₂，v＝x₁x₂で変数変換をすると容易に解ける場合がある。上の方程式は，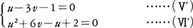

と書きかえられる。これは（1）と同じ方法で解けて，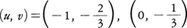
となる。二次方程式の根と係数の関係からx₁，x₂はt²－ut＋v＝0，すなわち，

の2根である。ゆえに，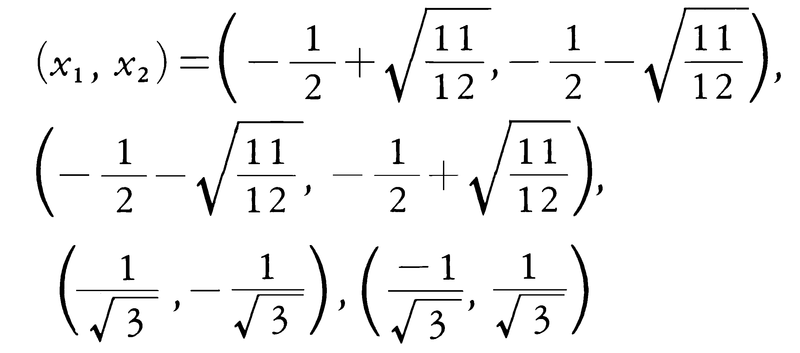

が解である。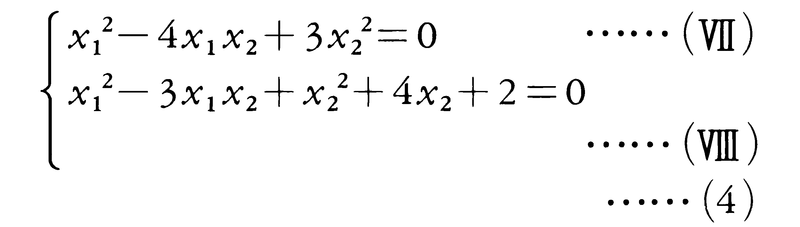

のように，一つの方程式がx₁，x₂についての斉次二次式であると，（x₁－3x₂）（x₁－x₂）＝0と因数分解されて，x₁＝3x₂またはx₁＝x₂となり，これも（1）に帰着する。その他の場合として，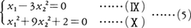

を考えると，x₁＝3x₂²を（Ⅹ）に代入して9x₂⁴＋9x₂²＋2＝0，この四次方程式は容易に解けて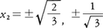，となる。一般に2変数で二つの二次式の場合には，一方の方程式をx₁について解いて，他方に代入すればx₂について四次式を得る。四次式の解法はわかっており，原理的には必ず解けるわけである。3変数，三つの二次式だと八次式が現れ，代数的には解けないことが多い。

　一般にf₁（x₁，……，x_n），……，f_r（x₁，……，x_n）のうちf_rのみが二次式のとき，連立二次方程式，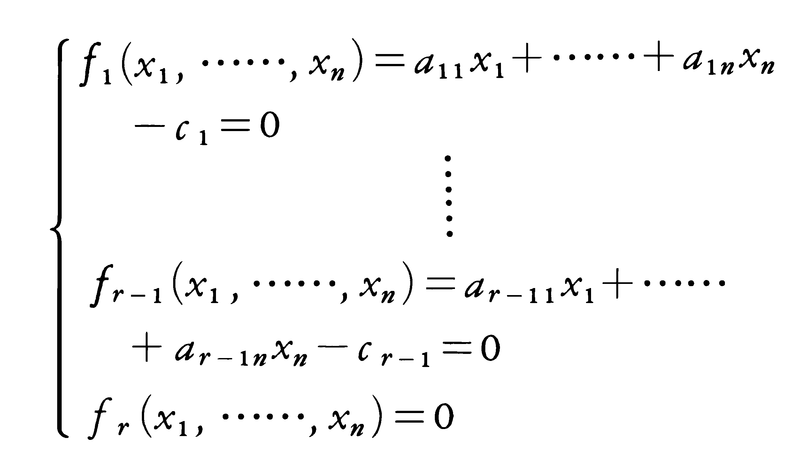

は容易に解ける。最初のr－1個の連立一次方程式を解いて，例えば，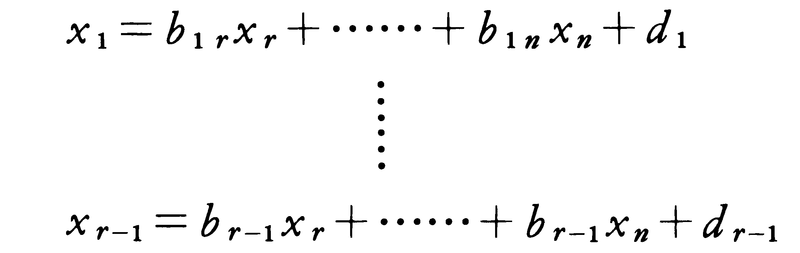

と書けたとする。この式をf_r（x₁，……，x_n）に代入すればx_r，……，x_nについての二次方程式を得るが，そのうちどれか，例えばx_rについての二次方程式とみて解けばx_rが定まる。前の式からx₁，……，x_r-1も定まる。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」