連立一次方程式（読み）れんりついちじほうていしき（英語表記）simultaneous linear equation

改訂新版　世界大百科事典

連立一次方程式 (れんりついちじほうていしき)
simultaneous linear equation

一次方程式の系，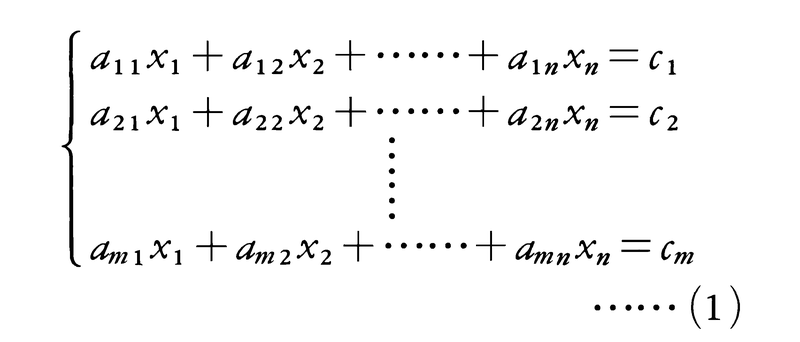

をn元連立一次方程式という。（x₁，……，

x_n）＝（a₁，……，a_n）が上のすべての一次方程式をみたすとき，（a₁，……，a_n）は（1）の解であるという。次の連立一次方程式を解いてみよう。

　3×（Ⅰ）－2×（Ⅱ）を作ると－y＝－2。したがってy＝2である。これを（Ⅰ）に代入して，x＝－3となる。この方法を加減法という。

　（Ⅰ）から，

を得る。これを（Ⅱ）に代入して，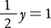

すなわちy＝2が得られる。（Ⅰ′）から，x＝－3となる。この方法を代入法と呼ぶ。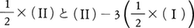を考えて，上の連立方程式は，

と同値である。2×（Ⅱ″）と（Ⅰ″）－\(\frac{5}{2}\)×（2×（Ⅱ″））を取れば，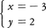

となる。これは掃出法といわれる。

　一般に，（1）の係数を要素とする行列，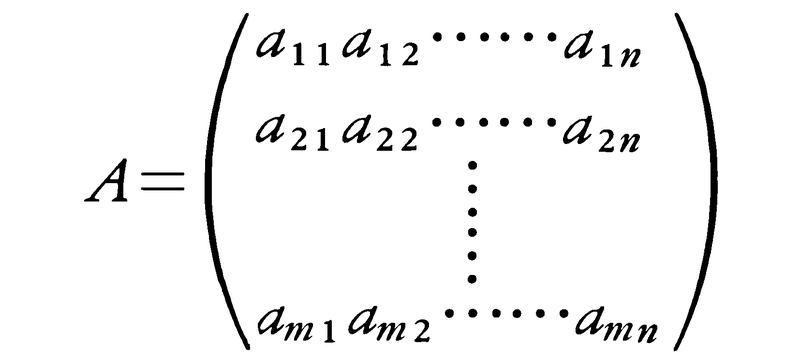

を（1）の係数行列といい，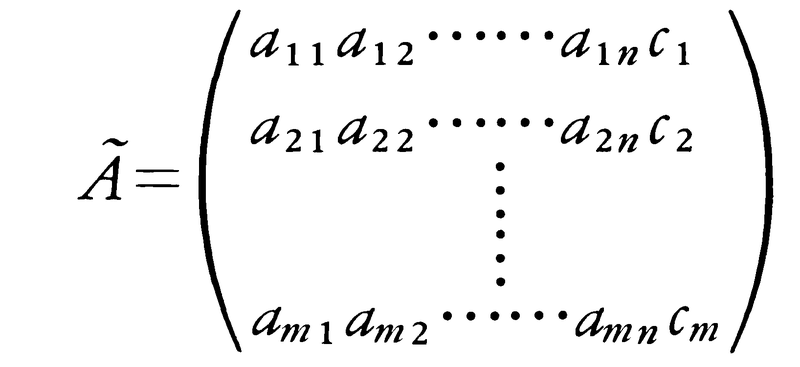

を（1）の拡大係数行列という。（1）のc₁，……，c_mが0である連立一次方程式，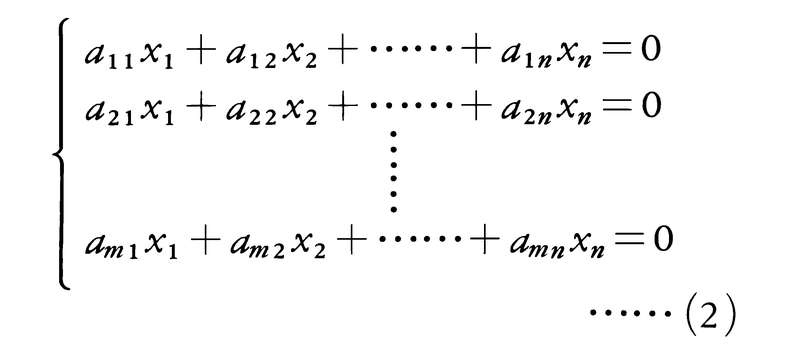

を斉次連立一次方程式という。（b₁，……，b_n），（b₁′，……，b_n′）が（2）の解ならば，任意のα，α′について，（αb₁＋α′b₁′，……，αb_n＋α′b_n′）も（2）の解になる。すなわち，斉次連立一次方程式の解全体は行ベクトルが作る線形空間の線形部分空間になる。係数行列Aの階数をrとすると，この部分空間の次元はn－rになる。（1）の解（d₁，……，d_n），（d₁′，……，d_n′）を取ると，（d₁－d₁′，……，d_n－d_n′）は（2）の解である。逆に，（d₁，……，d_n）が（1）の解ならば，（2）のかってな解（b₁，……，b_n）について，（d₁＋b₁，……，d_n＋b_n）は（1）の解である。したがって，（1）の解（d₁，……，d_n）を一つ取ってくれば，｛（d₁＋b₁，……，d_n＋b_n）｜（b₁，……，b_n）は（2）の解｝が（1）の解全体である。ところで，

　定理　（1）が解をもつための必要十分条件はAの階数とÃの階数が一致することである。

　（1）が解をもたないとき，（1）は不能であるという。また（1）が無限個の解をもつとき，（1）は不定であるということがあるが，上述のように解全体ははっきり定まるから，あまりよい言い方ではない。

　列ベクトル，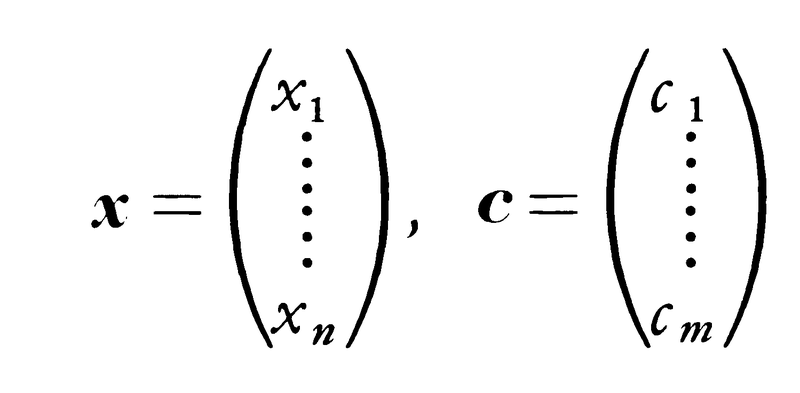

を取れば，（1）はAx＝cと書ける。今m＝nで，Aの行列式｜A｜が0でないとすると，Aは逆行列A⁻¹をもつ。上記の行列の式の両辺に左からA⁻¹をかけることにより，x＝A⁻¹cを得る。すなわち，連立一次方程式（1）はただ一つの解をもち，その解は上の式で書ける。この解を具体的に書くと，X_i＝｜A_i｜/｜A｜となる。ここで，A_iはAのi列をcで置きかえた行列，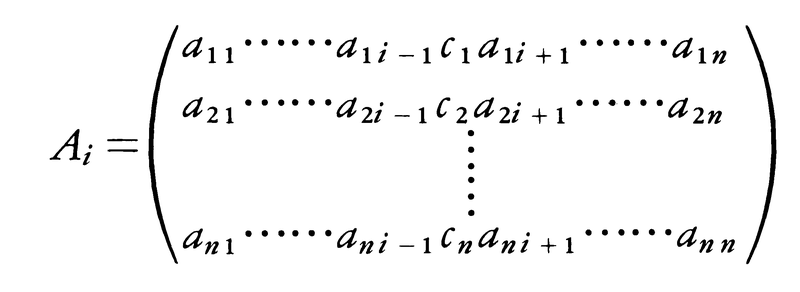

である。この解法をクラメールの方法と呼ぶ。実際に連立一次方程式を解くときは，クラメールの方法より，最初に述べた加減法，代入法，掃出法のほうが有効である場合が多い。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の連立一次方程式の言及

【数値解析】より

…(1)逆行列　Aをn次正則(行列式が0でない)行列とする。Aの逆行列A^－1を求めることは，x,yがn次元ベクトルで，yが任意に与えられたとするとき，連立一次方程式Ax＝yの解x＝A^－1yを求めることと同じである。A^－1の近似Cから出発することとし，　R＝1－CAとおく。…

※「連立一次方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」