精選版 日本国語大辞典 「対称」の意味・読み・例文・類語
たい‐しょう【対称】
- 〘 名詞 〙
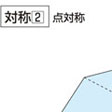
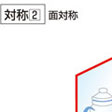
- ① 数学で、点対称、線対称、面対称の総称。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
- ② =たいしょうだいめいし(対称代名詞)〔語法指南(1889)〕
- ③ 物理学で、結晶面の間の規則正しい関係の一つ。結晶面のある面による鏡像、またはそれをある軸のまわりに回転させたものが、他の結晶面に一致する性質。〔稿本化学語彙(1900)〕
- ④ ( ━する ) 対応させて称すること。
- [初出の実例]「舞い手を立方というに対称して、地方と呼ばれる演奏者の立場にいても」(出典:地唄(1956)〈有吉佐和子〉)
- ⑤ 互いに対応しながらつりあうこと。また、ふさわしいこと。かなうこと。相称。
日本大百科全書(ニッポニカ) 「対称」の意味・わかりやすい解説
対称
たいしょう
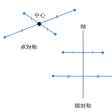
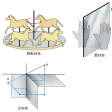
一定点に関して2点の中点がその定点であるとき、その2点を定点に関して互いに点対称であるという。一定直線に関して2点の垂直二等分線がその定直線と一致するとき、その2点は定直線に関して互いに線対称であるという。また、一定平面に関して2点の垂直二等分面がその定平面と一致するとき、その2点は定平面に関して互いに面対称であるという()。それぞれの場合、2点の一方を他の対称点という。
[柴田敏男]
平面図形の対称
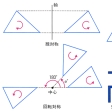
一つの平面図形を一定点の周りにα度回転してできる図形を、初めの図形にα度回転対称な図形といい、その定点を回転対称の中心という()。180度回転対称な二つの図形はその中心に関して点対称であるという。一つの図形の一定直線に関する対称点をとってできる図形を、初めの図形に線対称な図形といい、その定直線を線対称の軸という。線対称な二つの図形の対応する2点の垂直二等分線は、線対称の軸と一致する。回転対称では図形の向き(対応点を順次回る向き)は変わらないが、線対称では図形の向きが逆になる。回転対称や線対称になるようにする操作を回転対称移動、線対称移動という。平面でこれらの移動を考えると、回転対称ではその中心は動かない。線対称ではその軸上の点はすべて不動である。平面で図形の大きさを変えない移動はすべていくつかの線対称移動の繰り返しで求められる。たとえば平行移動は、二つの平行線を軸とする線対称移動の繰り返しであり、回転対称移動は、その中心を通る二つの直線を軸とする線対称移動の繰り返しである。
一つの平面図形がα度回転によって自分自身に重なるとき、その図形をα度回転対称な図形といい、回転の中心をその図形の回転対称の中心という。にあるような寺院の記号は90度回転対称な図形である。一つの図形が線対称移動により自分自身に重なるとき、その図形を線対称な図形といい、線対称の軸をその図形の対称軸という。二等辺三角形は、底辺の垂直二等分線を軸とする線対称な図形である。正多角形は回転対称かつ線対称な図形である。
[柴田敏男]
立体図形の対称
一つの立体図形を一定直線の周りにα度回転してできる図形を初めの図形にα度回転対称な図形といい、その定直線を回転対称の軸という()。一つの図形の一定平面に関する対称点をとってできる図形を、初めの図形に面対称な図形といい、その定平面を対称面あるいは鏡映面という。面対称な二つの図形の対応する2点の垂直二等分面は対称面と一致する。空間においても回転対称や面対称の移動を考えることができる。また、一つの図形の一定点に関する対称点をとってできる図形を、初めの図形に点対称な図形といい、その中心を点対称の中心というが、これは、初めの図形に三つの面対称移動を繰り返し施した結果になっている。
[柴田敏男]
改訂新版 世界大百科事典 「対称」の意味・わかりやすい解説
対称 (たいしょう)
symmetry
平面上または空間内に定点Oがあるとき,平面上または空間内の各点Pに対し,線分POの延長上にPO=OP′となる点P′をとって,PをP′にうつす対応を考える。この対応をOを対称の中心とする対称変換と呼び,対応する2点P,P′をOに関する対称点と呼ぶ。また,この変換で図形Fが図形F′にうつるとき,FとF′はOに関して点対称であると呼び,とくにF=F′のときFをOに関して点対称な図形という。例えば,円や球はそれらの中心に関して,平行四辺形や平行六面体は対角線の交点に関して点対称な図形である。平面上または空間内に定直線gがあるとき,平面上または空間内の各点Pに対し,Pからgに下ろした垂線の足をQとしてPQの延長上にPQ=QP′となる点P′をとって,PをP′にうつす対応を考える。この対応をgを対称軸とする対称変換と呼び,対応する2点P,P′をgに関する対称点という。また,この変換で図形Fが図形F′にうつるとき,FとF′はgに関して線対称であると呼び,とくにF=F′のときFをgに関して線対称な図形と呼ぶ。平面上の場合には,FとF′がgに関して線対称とはgを折り目として折り返したときにFとF′がまったく重なることを意味する。空間内に一平面πが与えられたとき,空間内の各点Pに対し,Pからπに下ろした垂線の足をQとしてPQの延長上にPQ=QP′となる点P′をとって,PをP′にうつす対応を考える。この対応をπを対称面とする対称変換と呼び,対応する2点P,P′をπに関する対称点という。また,この変換で図形Fが図形F′にうつるとき,FとF′はπに関して面対称と呼び,とくにF=F′のときFをπに関して面対称な図形という。鏡に写した顔はもとの顔と鏡の面に関して面対称といえる。平面上の図形Fが点Oのまわりの角αの回転によって自分自身に重なるとき,FはOに関して角αの回転対称であると呼ばれる。また,空間内の図形Fが直線gのまわりの角αの回転によって自分自身に重なるとき,Fはgに関して角αの回転対称であるという。例えば正方形は中心に関して90°の回転対称で,立方体はその対角線に関して120°の回転対称である。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
化学辞典 第2版 「対称」の解説
対称
タイショウ
symmetry
図形にある操作をほどこしたときに,操作の前後で図形が完全に互いに重なる場合にこの操作を対称操作とよび,この図形は対称であるという.二つの対称操作を引き続いて行ったものは,やはりある対称操作であって,対称操作の集合は群をつくり,それを対称群とよぶ.結晶や分子の形に関しては単位操作(何もしないこと),回転,回反(反転・鏡映を含む),並進ならびにそれらを組み合わせたものが対称操作となりうる.ある対称操作を定義するために記載上必要な点,軸,面またはその集合を対称要素または対称の要素という.対称要素には,独立した分子の場合には,対称心,回転軸,回反軸または回映軸,および対称面があり,結晶の場合には,このほからせん軸,映進面,空間格子がある.なお,より一般的には,任意個の独立変数 xi の関数f(xi)が定義されていて,xi の全部または一部にある変換や交換をほどこしたときに,関数値が変換・交換前と比較して同一の値または同一の主値をとる場合に,f(xi)はこの関数の変換や交換に関して対称であるといい,変換などによって符号のみが変わる場合を反対称であるという.物体の場合でも,双極子や波動関数の分布については,反対称の対称要素や変換を考えることができる.誘電性,圧電性などの物性の記述には対称の概念が不可欠である.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
最新 地学事典 「対称」の解説
たいしょう
対称
symmetry
(1)一つの平面図または立体図形について,その中点または中心を通る架空の線・平面および点(中心そのものになる)を考え,これらに関して前に述べた図形にある操作または運動を加えたとき,その図形が操作以前とまったく同じ空間を占める(すなわち操作を加えない前と同じ状態になる)とき,これらの図形は対称をもつという。壁紙・テーブルクロス・橋・ビルディングなど,われわれの周囲にも対称をもった製品や構築物は多い。そして,これらを重ね合わせるための幾何学的操作により点対称・線対称・面対称・軸対称などと呼ばれる。結晶の形態および結晶の原子配置などにもこのような対称が見いだされる。[高野 幸雄]
(2)ファブリック要素の統計的空間配列の対称は結晶格子の対称と類似し,空間群の対称の一種である。次の五つの対称が認められている(B.Sander, 1930, 48;M.S.Patterson et al.,1961)。a.球対称ファブリックK∞h。ファブリック要素が乱雑に向いている場合。例えばホルンフェルス中の鉱物の配列。b.軸対称ファブリックD∞h。ファブリック要素の配列が1本の軸で交わる無数の対称面とそれに垂直な対称面の存在を示す場合。c.斜方対称ファブリックD2h。互いに直角な三つの対称面が存在する場合。d.単斜対称ファブリックC2h。ただ一つの対称面が存在する場合。e.三斜対称ファブリックS2=Ci。対称面がまったく存在しない場合。
執筆者:小島 丈児
出典 平凡社「最新 地学事典」最新 地学事典について 情報
百科事典マイペディア 「対称」の意味・わかりやすい解説
対称【たいしょう】
→関連項目双晶|相称|対称要素
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「対称」の意味・わかりやすい解説
対称
たいしょう
symmetry
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
普及版 字通 「対称」の読み・字形・画数・意味
【対称】たいしよう
字通「対」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
世界大百科事典(旧版)内の対称の言及
【結晶】より
…点Oにおける測定値のベクトルの先端の図形は,aではOの周りに180度回転しないと最初に与えられている図形とは一致しないが,bでは90度回転ごとに最初のものに重なる。このように,ある図形(あるいは物体)Xを動かして最初の形に重ね合わせることをXの対称操作といい,Xのもつすべての対称操作の集りをXの対称symmetryという。対称操作を具体的に表すものを対称要素という。…
※「対称」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...