改訂新版 世界大百科事典 「連続写像」の意味・わかりやすい解説
連続写像 (れんぞくしゃぞう)
continuous mapping
f:X→Yを集合Xから集合Yへの写像とする。すなわちXの各点xに対しYの点f(x)が対応しているとする。もし集合X,Yのいずれもが“近い”とか“近づく”といった概念で表される構造,すなわち位相構造を備えていれば,写像fがXの点aで連続であるという概念が定義できる。すなわち,〈Xの点xがaに近くなれば,f(x)がf(a)にいくらでも近くなる〉という条件によってそれを定義するのである。そして,〈fがXの各点で連続であるとき,写像f:X→Yは連続である〉と定義することにより,連続写像という概念が得られる。以上が連続写像のおおまかな説明であるが,fが点aで連続であるということを厳密に定義すると次のようになる。微積分学でよく知られているように,区間Iで定義された実数値関数,すなわちIから数直線Rへの写像f:I→RがIの点aで連続であるというのは,〈任意の正数εに対して,正数δを適当に選ぶと,|x-a|<δならば|f(x)-f(a)|<εとなる〉ことである。X,Yが距離によって位相が与えられる距離空間の場合には,上の定義にならって,f:X→YがXの点aで連続であるとは,〈任意の正数εに対して,正数δを適当に選ぶと,d(x,a)<δならばd(f(x),f(a))<εとなる〉ことであると定義する。なおここでd(x,a)はXにおけるxとaの距離,d(f(x),f(a))はYにおけるf(x)とf(a)の距離を表す。一般に,距離空間Xの点xと正数εに対し,xからの距離がεより小さいようなXの点全体の集合Uε(x)はxのε近傍と呼ばれる。この概念を用いると上の定義は〈任意の正数εに対して,正数δを適当に選ぶと,x∈Uδ(a)ならばf(x)∈Uε(f(a))となる〉と換言される。ここで,εを与えてδを選ぶとは,f(a)の近傍を与えてaの近傍を選ぶことにほかならないことに注意するとき,位相が近傍ということばによって与えられる位相空間の場合の次の定義が生まれる。位相空間Xから位相空間Yへの写像f:X→YがXの点aで連続であるとは,〈f(a)の任意の近傍V(f(a))に対し,aの近傍U(a)を適当に選ぶと,x∈U(a)ならばf(x)∈V(f(a))となる〉ことである。
これで連続写像の概念がもっとも一般な位相空間の場合に厳密に定義されたわけであるが,これに関する次の定理は基本的である。〈位相空間Xから位相空間Yへの写像f:X→Yに対し,次の4条件は同値である。(1)fは連続である。(2)Yの任意の開集合Oに対しf⁻1(O)はXの開集合である。(3)Yの任意の閉集合Cに対しf⁻1(C)はXの閉集合である。(4)Xの任意の部分集合Aに対して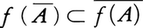 。ここに-はそれぞれの位相空間における閉包を表す〉。二つの連続写像の合成は連続写像である。連続写像f:X→Yが1対1対応を与えても,逆写像f⁻1:Y→Xは連続写像とは限らない。f⁻1も連続であるときfを同相写像(位相写像)といい,このようなfが存在するときXとYは同相(位相同型)であるという。
。ここに-はそれぞれの位相空間における閉包を表す〉。二つの連続写像の合成は連続写像である。連続写像f:X→Yが1対1対応を与えても,逆写像f⁻1:Y→Xは連続写像とは限らない。f⁻1も連続であるときfを同相写像(位相写像)といい,このようなfが存在するときXとYは同相(位相同型)であるという。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

