位相空間（読み）イソウクウカン（英語表記）topological space

デジタル大辞泉

いそう‐くうかん〔ヰサウ‐〕【位相空間】

１ 数学で、位相の概念が導入された空間（点集合）。
２ 物理学で、物体の力学系の物理的状態を表すための、その物体の位置と運動量を座標とする多次元空間。

出典　小学館

精選版 日本国語大辞典

いそう‐くうかんヰサウ‥【位相空間】

1. 〘 名詞 〙
2. ① ( [英語] topological space の訳語 ) 数学で、位相の定義された集合。この空間では点列の収束や、関数の連続性などを論ずることができる。
3. ② 物理学で、位置を指定する一般化座標に、これと対応する一般化運動量の概念を導入して、力学系の任意の状態を代表できるように位相づけられた抽象空間。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

位相空間 (いそうくうかん)
topological space

実数の集合や平面上の点集合には“近さ”とか“近づく”といった概念で表される構造が備わっているので，これを用いることにより，これらの集合上では極限や連続の概念が定義される。一般の集合についても，それにある種の構造を与えることにより，極限や連続などの概念が定義でき，これらについての理論を展開することが可能となる。このような構造を位相といい，位相の与えられた集合を位相空間という。平面上の点集合のように，2点間に距離が定義されている距離空間Eでは，距離の概念を用いて“近さ”や“近づく”といった概念が定義され，位相が定まる。すなわち，Eの点列a₁，a₂，……，a_n，……がEの点aに収束するとは，nが大きくなるにつれてa_nとaとの距離がしだいに小さくなることであると定義し，EからEへの写像fがEの点aで連続とは，Eの点列a₁，a₂，……，a_n，……がaに収束するならば，f（a₁），f（a₂），……，f（a_n），……はf（a）に収束するという条件が成り立つことであると定義すればよい。しかしながら，近さの概念は距離の概念に先立つ存在で，“近い”ということのもつ基本的性質をとり出すことによって，位相が距離による方法よりもっと一般的な方法で与えられる。これをみるため，まず平面上の点集合Eを考察しよう。UをEの部分集合とし，aはUの1点とする。いま，Uがaの近傍であるとは，十分小さい正数εをとるとき，aからの距離がεよりも小さい点はすべてUに含まれることであると定義すれば，容易に次の3性質の成り立つことがわかる。（1）aの近傍Uはaを含む。（2）U₁，U₂がaの近傍ならば，U₁にもU₂にも含まれるようなaの近傍U₃がとれる。（3）Uがaの近傍ならば，Uの各点bに対し，Uに含まれるようなbの近傍Vがとれる。このことより抽象して，一つの集合Sに位相を与えるとは，Sの各点aに対しSの部分集合の族を定め，これらの部分集合をaの近傍と呼ぶとき，上の3性質が成り立つようにすることであると定義する。このように定義された位相空間Sでは，Sの点列a₁，a₂，……，a_n，……がSの点aに収束するとは，aのどんな近傍Uをとっても，あるところから先のすべてのa_nはUに含まれることであると定義され，また，SからSへの写像fがSの点aで連続とは，f（a）のどんな近傍Vに対しても，aの近傍Uでf（U）はVに含まれるようなものがとれることであると定義される。位相空間S，S′に対し，SからS′の上への1対1写像fで，fおよびその逆写像f⁻¹がともに連続であるようなものが存在すれば，SとS′は同位相または同相であると呼ばれる。一つの集合に対し，一般に，いろいろの異なった位相を与えることができる。Sを位相空間，Aをその部分集合とし，xをSの点とするとき，xの任意の近傍がx以外にAの点を含むならば，xをAの集積点accumulation pointといい，xのある近傍がAに含まれるならば，xをAの内点という。Aがそれの集積点をすべて含むならばAを閉集合closed setといい，Aの点はすべてそれの内点ならばAを開集合open setという。これらの概念は位相空間論で基本的で，これらの概念のいずれか一つから出発しても位相空間を定義することができる。
執筆者：中岡 稔

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

位相空間
いそうくうかん
topological space

集合のなかに連続性を議論するもとになる位相という構造が導入されたものを位相空間という。この集合を一つ固定し、そのなかでいろいろな議論を展開していくため、この集合を空間、その各要素を点とよぶ。位相的な概念としては、開集合、閉集合、集積点、近傍(きんぼう)、収束などがあり、空間に位相を導入する方法も、これら諸概念に応じていろいろある。次に開集合による導入の仕方を示す。

　空間Sに、次の性質をもつSの部分集合の集まり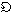が付与されているとき、Sに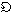を開集合族とする位相が与えられたという。

(1)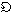は全空間Sおよび空集合∅を含む。

(2)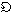に属する二つの集合の共通部分はまた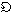に属する。

(3)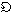に属する集合（どれだけたくさんあってもよい）の和集合は、また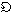に属する。

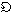　に属する集合を開集合という。Sの相異なる2点p、qに対して、pを含む開集合Uとqを含む開集合Vを適当にとれば、両者が交わりをもたないようにできる(U∩V＝∅)とき、Sをハウスドルフ空間といい、この性質をもつ空間を議論することが多い。

　位相空間Sの部分集合Mは次の性質をもつとき、コンパクトであるという。「開集合の集まりでその全体の和集合がMを含んでしまうようなものを考えるとき、いつでも、そのうちの適当な有限個をとればすでにその和集合がMを含んでいる」。コンパクト性は位相空間の性質を論ずる際にもっともよく用いられる重要な概念である。また、二つの位相空間S、Tの間の写像f：S→Tが連続であるのは、Tの開集合のfによる原像がつねにSの開集合となる、という性質をもつときである。

　位相空間の例をあげよう。数直線では、集合Oが開集合であることを次のように定義する。すなわち、Oに属するどの点pに対しても、Oに含まれpを含む区間がとれるときである。このようにして定めた開集合の全体を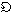とすれば、数直線は位相空間となる。これが位相空間の原型である。次に、空間Sの2点p、qに対して定義された関数d（p，q）が、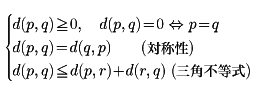

の性質を有するとき、これをS上で定義された距離関数といい、距離関数の付与された空間を距離空間という。たとえば、座標平面では、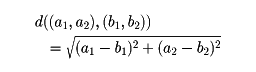

のようにとれば距離関数が得られ、距離空間となる。したがって距離空間とは、数空間の考察を一般化したものといえる。距離空間では、点pに対し、
　　V=｛q：d(p，q)＜ε｝
の形の集合をpのε(イプシロン)近傍という。そして、集合Oが開集合であることを、数直線の場合と同様に、Oのどの点pに対してもOに含まれるようなpのあるε近傍があること、と定義すれば、Sは位相空間（ハウスドルフ空間）となる。

　位相的な概念が初めて一般的な形で登場したのはカントルによる（1872）。彼は数直線において、集積点や導集合の考えを導入し議論した。一般の空間に位相を導入する議論に初めて成功したのはハウスドルフである（1915）。ついでクラトフスキー（1922）、ベーユやカルタンやバーコフ（1937）らによって位相の導入のいろいろな仕方が与えられた。

［竹之内脩］

『竹之内脩著『集合・位相』（1970・筑摩書房）』

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

位相空間(数学)【いそうくうかん】

極限や連続の概念が定義できる集合のうち最も一般的なもの。集合Xの部分集合の族θで以下1.〜3.の条件を満たすものが一つ指定されているとき，Xを位相空間，θの元をXの開集合という。1.θに属する任意個の集合A(/i)の和集合∪A(/i)もθに属する，2.θに属する任意の集合A₁，A₂の共通部分A₁∩A₂もθに属する，3.Xおよび空集合φがθに属する。集合Xに対しこのようなθを定めることを，Xを位相づけるといい，θをXの位相と呼ぶこともある。実数の全体は一次元の位相空間。→位相幾何学／位相数学
→関連項目空間（数学）｜次元（数学）｜点

位相空間(物理)【いそうくうかん】

ある力学系の位置を指定する一般化座標q₁，q₂，q₃，……，q(/f)と，これに対する一般化運動量（運動量）p₁，p₂，p₃，……，p(/f)を直角軸にとった２f次元の空間。力学系の状態はこの空間内の一点（代表点）で表され，代表点は系の運動に従って空間内を移動する。力学，統計力学，量子力学などで利用される。

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

位相空間
いそうくうかん

(1) phase space　力学系の状態を記述するために考えられた空間。一般に座標 q_i(i＝1，2，…，f) とそれらに共役な運動量 p_i(i＝1，2，…，f) を座標にもつ 2f 次元空間。系の力学的状態は位相空間内の1点で代表され，力学系の運動に対応して，代表点は時間とともに位相空間の中を移動する。統計力学の分野では Γ 空間と呼ぶこともある。気体分子の運動を例にとると，この気体全体の状態が Γ 空間の1点で代表される。1個の分子の状態に対応する位相空間をμ空間という。 (2) topological space　解析学で大切な連続や極限の概念は一般の抽象空間においても定義できる。このような定義を可能とする抽象空間の構造を，位相という。空間の各点に基本近傍を対応させ，基本近傍の集合である近傍系によって位相づけられた空間を位相空間と名づける。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の位相空間の言及

【位相幾何学】より

…
［位相幾何学の現状］
　20世紀の数学は，その位相性と代数性を基礎として，公理的に構成されている。連続性が議論できる空間は位相空間といい，図形も一種の位相空間である。位相を定める基本的諸概念は近傍，開集合，閉包などである。…

【解析力学】より

…正準形式の重要な点は(2)の構造が相対論にももち越されることで，上例で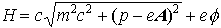，とすることで確かめられる(cは光速度)。
［相空間］
　正準変数q₁，……，q_f；p₁，……，p_fの作る2f次元ユークリッド空間を相空間または位相空間phase spaceといい，(2)の解はこの空間における軌道群(異なる軌道は異なる初期値に対応)で表されるが，次のような基本的性質が備わっている。(a)体積不変性　体積Vの任意の領域を取り，その中の点すべてを(2)に従って追跡したとき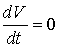(b)密度不変性　(2)に従う力学系の集団を考え，密度関数ρ(t,p,q)によって分布しているものとすると，上と同じ領域に出入りする(状態)点の総和はつねに0に保たれる。…

【統計力学】より

…自由度nの系の微視的状態は，一般化座標q₁,q₂，……，q_nおよびこれらに正準共役な運動量p₁,p₂，……，p_nによって指定する。ある時刻tにこれら2n個の量がとる値の組を系の位相と呼び，可能な位相の集合である2n次元ユークリッド空間を位相空間という(この位相空間をP.エーレンフェストはΓ空間と呼んだ)。この空間内の確率分布ζ(q₁，……，q_n,p₁，……，p_n,t)の形で統計集団が規定される。…

【ボルツマン方程式】より

…この分布を記述するため，時刻tにおいて，座標がx～x＋dx,y～y＋dy,z～z＋dzの範囲内，また運動量成分がp_x～p_x＋dp_x,p_y～p_y＋dp_y,p_z～p_z＋dp_zの範囲内にあるような分子数を，　f(x,y,z,p_x,p_y,p_z,t)　　×dxdydzdp_xdp_ydp_zとおく。このような関数fを位相空間における分布関数という。ちなみに，座標と運動量とから構成される空間が位相空間phase spaceである。…

※「位相空間」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」