微積分学（読み）ビセキブンガク（その他表記）differential and integral calculus

デジタル大辞泉

びせきぶん‐がく【微積分学】

微分と積分、および両者の関連などの理論を研究する学問。

出典　小学館

精選版 日本国語大辞典

びせきぶん‐がく【微積分学】

1. 〘 名詞 〙 微分と積分とに関する数学的理論。微分に関する微分学、積分に関する積分学、および微分と積分との関連を論じる部分から成る。微分積分学。微積分。微積。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

微積分学 (びせきぶんがく)
differential and integral calculus

微積分学は微分学（微分法）と積分学（積分法）とを合わせた名称であるが，この二つは別々に考えるべきではなく，いっしょに考えるべき数学の体系であるから，両方を合わせて微積分学，あるいは略して微積分という。微積分は1670年ころにI.ニュートンとG.W.ライプニッツによってほとんど同時に発見された。発見の当初には，2人のうちどちらの発見が早かったか，またどちらかが他方の発見を知っていたのではないかということについて，激しい論争があった。当時は現在のように研究の結果が直ちに印刷公表されて多くの人に知らされるという時代ではなかったので，このような問題が起こったが，その後の数学史家の調査によって，2人の発見はまったく独立に行われたことがわかった。

　微分法と積分法は，それぞれの萌芽はずっと以前からあった。微分法の概念の起りは速度や接線の概念である。17世紀前半には，曲線の接線を求めることがP.deフェルマー，R.デカルトらによって研究され，さらに関数の極大値や極小値の求め方がフェルマー，B.パスカルによって考えられた。積分の概念は求積（面積や体積を求めること）の問題に始まり，ギリシア時代から扱われた。ユークリッドの有名な《ストイケイア》には円錐，角錐の体積が求められているが，これはエウドクソスによるものといわれる。アルキメデスはさらにいろいろの平面図形の面積，立体の体積や重心を求めている。しかもエウドクソス，アルキメデスはいずれもその結果に厳密な証明を与えている。近世になって求積の問題を扱ったのはB.カバリエリが最初で，フェルマー，パスカルなどがこれに続く（いずれも17世紀前半）。しかし，これらの人々の方法は，接線を求める問題でも求積の問題でも，個々の問題に対してそれぞれのくふうをするものであった。ニュートンとライプニッツの功績は，このような問題を解く一般的な方法を発見し，また微分法と積分法とが互いに逆の演算であることを明らかにしたことである。ニュートンの微積分によって，惑星の運動に関するケプラーの3法則が万有引力の法則（いわゆる逆2乗の法則）から導き出され，また逆2乗の法則がケプラーの3法則から演繹された。なお，現在の微分を表す記号dや積分を表す記号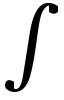はライプニッツの用いたものである。

　微積分は数学史上最大の発見といわれ，現在では，この発見の影響を受けていない数学の領域はないといえる。数学に限らず，自然科学，工学，医学などに与えた影響も大きい。微積分学では，独立変数の値の変化に対する関数の値の変化の状態を，導関数という概念で明確にとらえ，導関数を求める方法を調べて，これをいろいろな問題に応用する。与えられた関数からその導関数を求める演算が微分法であり，逆に，与えられた関数を導関数とするような関数を求める演算が積分法である。たとえば，運動する点の位置の座標が時間の関数として与えられたとき，その点の速度や加速度を求めること，与えられた関数の極大値・極小値を求めることは，微分法の問題として解かれ，また，与えられたいくつかの関数のグラフで囲まれた平面の部分の面積を計算したり，与えられた関数のグラフの長さを計算することなどは，積分法によって解かれる。微積分の数学的な内容については，〈微分〉〈積分〉などの項目を参照されたい。未知関数の導関数を含む方程式を微分方程式というが，微分方程式を解くことは微積分の直接の応用であって，現在では微積分学という名称の中に微分方程式の初等的理論や解き方を含めることもある。自然現象や自然の法則は微分方程式で記述されるものがきわめて多い。このことが，微積分が自然科学や工学などに対して大きな影響を与えてそれらを発展させた理由である。

　19世紀の中期から，微積分学はA.L.コーシー，G.F.B.リーマン，K.ワイヤーシュトラスらによって，複素変数の関数を対象とする解析関数論へと一般化の方向をたどって発展していった。この分野は通常単に関数論と呼ばれ，今もなお新しい研究が生まれている。一方，これと並んで，微積分学の基礎的諸概念を確立し精密にするという方向にも発展することにより，実関数論（実変数関数論）と呼ばれる分野が生じ，フーリエ級数の理論からフーリエ解析へと進んだ。20世紀に入り，積分の概念がそれまでのリーマン積分からルベーグ積分に拡張され，それを応用することにより，フーリエ解析の理論を含む関数解析学が起こった。関数解析学はそれまでの微分方程式や積分方程式などの解析学の諸理論を統一的な方法で考察することを可能にするとともに，それらをさらに発展させ，微積分学のうえに立って解析学の基礎と応用を支えているといえる。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

微積分学【びせきぶんがく】

→微分積分学

出典　株式会社平凡社

日本大百科全書(ニッポニカ)

微積分学
びせきぶんがく

→微分積分法

出典　小学館　日本大百科全書(ニッポニカ)