ブリタニカ国際大百科事典 小項目事典 「スペクトル定理」の意味・わかりやすい解説
スペクトル定理
スペクトルていり
spectrum theorem
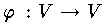 を対称線形写像とすれば,V には
を対称線形写像とすれば,V には 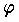 の固有ベクトルから成る直交基底が存在する。この事実をスペクトル定理といい,このような性質をもつ基底をスペクトル基底という。これはヒルベルト空間での同じような定理の特別の場合であり,ヒルベルト空間のスペクトル定理は,積分方程式の固有値問題から始った。有限次元の場合には,固有値は有限個で,離散的な点スペクトルであるが,無限次元のヒルベルト空間では連続スペクトルが現れ,有限次元の類比ではすまない。
の固有ベクトルから成る直交基底が存在する。この事実をスペクトル定理といい,このような性質をもつ基底をスペクトル基底という。これはヒルベルト空間での同じような定理の特別の場合であり,ヒルベルト空間のスペクトル定理は,積分方程式の固有値問題から始った。有限次元の場合には,固有値は有限個で,離散的な点スペクトルであるが,無限次元のヒルベルト空間では連続スペクトルが現れ,有限次元の類比ではすまない。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報

