固有値（読み）コユウチ（その他表記）eigenvalue

デジタル大辞泉

こゆう‐ち〔コイウ‐〕【固有値】

ベクトルを一次変換したとき、もとのベクトルの何倍になったかを示す値。Aを正方行列（一般に一次変換を表す）とするとき、Ax＝λxとなるベクトルxをλに属する固有ベクトル、λをAの固有値という。

出典　小学館

精選版 日本国語大辞典

こゆう‐ちコイウ‥【固有値】

1. 〘 名詞 〙 数学で、行列に付随する値の一群。Ａを正方行列、Ｅを単位行列、ｘを変数とするとき、A-xE の行列式を０とおいてえられるｘの方程式の根をＡに対していう。固有ベクトル。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

固有値
こゆうち
eigenvalue

複素数（実数の場合を含む。以下同様）を成分とするn次正方行列A＝(a_ij)と複素数λに対して、
　　〔1〕　Ax＝λx
を満たすゼロベクトルでないn次列ベクトル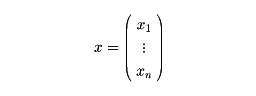

があるとき、λを行列Aの固有値といい、xをAの固有値λに対する固有ベクトルという。たとえば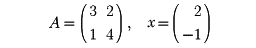

とすれば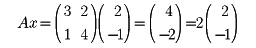

であるから、λ＝2はAの固有値で、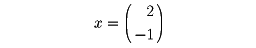

はλ＝2に対する固有ベクトルである。与えられた正方行列の固有値と固有ベクトルを求める問題を固有値問題という。

　E_nをn次単位行列とすると、〔1〕式は
　　〔2〕　(λE_n－A)x＝0
となる。n次正方行列(λE_n－A)で複素数λを変数tに置き換え、n次正方行列(tE_n－A)をつくる。その行列式

を行列Aの固有多項式または特性多項式という。この多項式ψ_A(t)は、(1)次数nで最高次の係数1、(2)t^n-1の係数は －traceA＝－(a₁₁＋a₂₂＋……＋a_nn)、(3)定数項は(－1)ⁿdetAなる変数tの多項式である。たとえば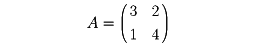

に対して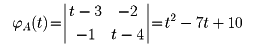

である。

　与えられた正方行列Aと複素数λに対して、未知数x₁、x₂、……、x_nの連立一次方程式〔2〕がゼロ解以外の解をもつ必要十分条件は
　　det(λE_n－A)＝ψ_A(λ)＝0
であるから、行列Aの固有値は固有多項式ψ_A(t)の根と一致する。したがって固有値問題は次の手順で解ける。まず固有多項式ψ_A(t)をつくり、その根λ₁、λ₂、……、λ_nを求め、次に、各λ_iに対して連立一次方程式(λ_iE_n－A)x＝0のゼロ解でない解xを求め、Aの固有値λ_iとそれに対する固有ベクトルxを得る。たとえば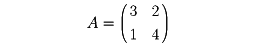

に対して固有多項式はψ_A(t)＝t²－7t＋10で、その根はλ₁＝2、λ₂＝5である。λ₁に対して、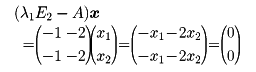

の解は－x₁－2x₂＝0であるから、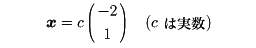

の形をしており、c＝－1としたものが冒頭の例である。同様にλ₂に対して、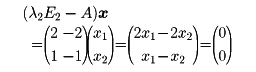

の解は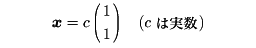

の形をしており、たとえばc＝1とした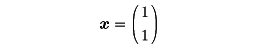

はλ₂に対する固有ベクトルである。

　このように、n次正方行列Aの固有値はたかだかn個であるが、各固有値λに対する固有ベクトルは無数にある。W_λを、行列Aの固有値λに対する固有ベクトル全体と0（ゼロベクトル）のつくる集合とする。W_λはn次元ベクトル全体のつくる線形空間Cⁿの部分空間である。W_λを行列Aの固有値λに対する固有空間という。

　n次正方行列A、Bに対し、n次正則行列（すなわち逆行列の存在する行列）PがあってB＝P^-1APとなるとき、AとBは相似であるという。たとえば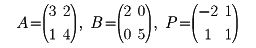

とすると、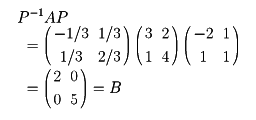

であるから、AとBは相似である。相似関係は同値関係である。相似である二つの正方行列は共通の固有多項式をもち、したがって固有値は一致する。さらに共通の固有値に対する固有空間の次元は等しい。このように相似である行列は行列としての重要な性質を共有するから、与えられた正方行列Aに対し、より簡単な行列BでAに相似であるものをみつけることが有力な研究手段になる。これについては、行列Aが対角行列に相似であるためには、Aの各固有値に対し、固有空間W_λの次元が固有多項式ψ_A(t)における根λの重複度に一致することが必要十分条件であり、とくにAの固有値がすべて相異なるとき、Aは対角行列に相似であることが知られている。

　複素線形空間Vの線形変換Tと複素数λに対し、T(x)＝λxを満たすようなゼロ元でないVの元xがあるとき、λを線形変換Tの固有値といい、xをTの固有値λに対する固有ベクトルという。固有ベクトルxはTによって方向の変わらないベクトルである。線形変換に対しても行列と同様に固有値問題が考えられるが、Vの基底e₁,……, e_nをとり、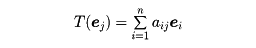

なるa_ijで正方行列A＝(a_ij)をつくると、TとAの固有値は一致し、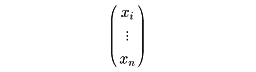

がAの固有値λに対する固有ベクトルなら、x₁e₁＋……＋x_ne_nはTの固有値λに対する固有ベクトルで、逆も成り立つから、線形変換Tの固有値問題は、完全に行列Aの固有値問題に帰着される。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

固有値 (こゆうち)
eigenvalue

X，Yは線形空間でYはXを部分空間として含むものとし，LをXからYへの線形作用素とするとき，Lu＝λu（λは定数）となるようなu∈Xがu＝0以外に存在するとき，λをLの固有値，uをそれに対応する固有ベクトル（Xが関数空間である場合には固有関数）といい，固有値および固有ベクトルを求める問題を固有値問題という。いくつかの具体例をあげよう。

（1）Xがn次元ベクトル空間で，XからXへの線形作用素Lが行列（a_ij）で与えられているとき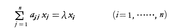，を満たすような0でないベクトル（x₁，……，x_n）が存在すれば，λはLの固有値である。それは特有方程式（または特性方程式）と呼ばれるn次方程式，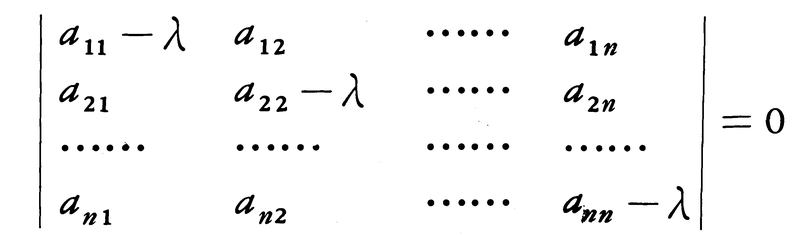

の根として与えられる。

（2）Xを閉区間［a，b］上の連続関数全体のつくる線形空間，K（x，ζ）をa≦x≦b，a≦ξ≦bで連続な関数とし，XからXへの線形作用素Lを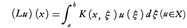，と定義する。Lをフレドホルム型の積分作用素，K（x，ξ）をその核と呼ぶ。このとき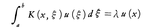，を満たす恒等式に0でない関数u∈Xが存在すれば，λはLの固有値である。ただし積分作用素の場合には，歴史的理由で，1/λを固有値と呼ぶことがしばしばあるので注意を要する。

（3）閉区間［a，b］上で2階連続微分可能な関数u（x）で，条件，

　αu（a）＋α′u′（a）＝0，

　βu（b）＋β′u′（b）＝0

　　　　　　　　（α，α′，β，β′は定数）

を満たすものの全体をX，［a，b］上で連続な関数の全体をYとし，LをXからYへの2階線形微分作用素，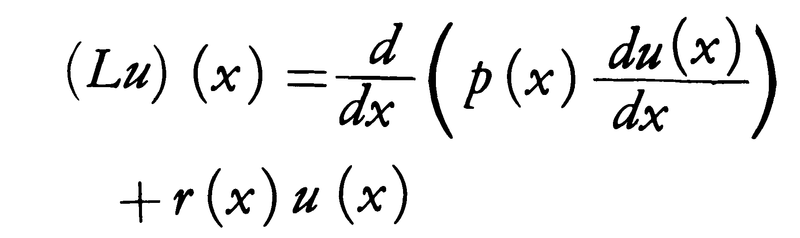

とする。このとき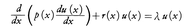，を満たすような，恒等的に0でない関数u∈Xが存在すれば，λはLの固有値である。

　固有値問題（2）はフレドホルムE.I.Fredholm（1866-1927）によって完全に解決されており，固有値問題（3）は（2）に帰着できることがわかっている。
執筆者：斎藤 利弥

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

固有値
コユウチ
characteristic value, proper value, eigen value

その自乗積分が有限で1であるような条件をつけられた関数につき，ある微分方程式が成り立つとき，方程式中のあるパラメーターの特別な値に対してのみ上の条件を満たす解が得られることを微分方程式の固有値問題といい，パラメーターの特別な値を固有値，それに対する解を固有関数という．量子力学におけるシュレーディンガーの波動方程式の解である波動関数，つまり状態関数も上記の固有値問題として方程式に含まれる系のエネルギーEのある特別の値に対してのみ解が得られる．これが原子系がとびとびの値のエネルギーをもつことの理由となる．たとえば，質量mの粒子が振動数νで変位xの一次元振動を行うとする．位置のエネルギーは，

V(x) ＝ 2π ²ν ²mx ²

である．いま，

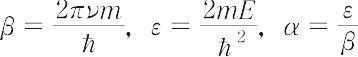
として，xから

ξ 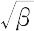＝ x
に変数変換を行うと，系の波動関数φ(x)に対するシュレーディンガーの方程式は，

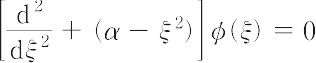
という形になる．Cを定数とし，

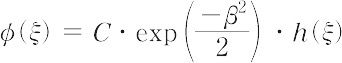
とおくと，h(ξ)は，

h″(ξ) － 2ξ･h′(ξ) ＋ (α － 1)h(ξ) ＝ 0

を満たさなければならないことがわかる．φ(x)が自乗積分可能で，

∫_－∞^∞φ (x)²dx ＝ 有限 ＝ 1

であるためには，h(ξ)が，

h(ξ) 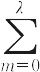＝ a_λξ^λ

のように定数 a₀ あるいはa₁ξからはじまり，ξ^λ とξの有限次項で終わる関数であればよい．ところがもし

α － 1 ＝ 2λ，
ただし，

λ ＝ 0，1，2，…正整数
であるならば，h(ξ)の微分方程式は，

H″(ξ) － 2ξH′(ξ) ＋ 2λH(ξ) ＝ 0

となるが，この解はエルミートの多項式H_λ(ξ)といわれるものとなる．H_λ(ξ)はλの偶奇に対応し，ξの0，2，4，…，λ乗までの多項式かξの1，3，5，…，λ乗までの多項式となり，上のφ(x)の自乗積分可能の条件をも満たしている．したがって，固有値の条件は，

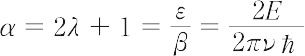
であり，これはエネルギーEが固有値，

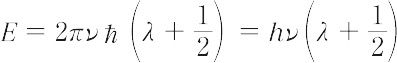
を示している．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

固有値
こゆうち
eigenvalue; primitive root

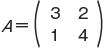固有根，あるいは特有値，特有根ともいう。 A＝(a_ij) を n 次の正方行列とするとき，Ax＝λx ( x は 0 でないベクトル，λ は定数) をみたす x を固有ベクトル，λ を固有値という。そのための条件は λ が n 次代数方程式 ｜A－λI｜＝0 の解であることである。この方程式を行列 A の固有方程式または永年方程式という。たとえば， の固有値 λ は
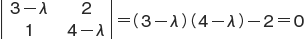の根であるから，λ＝2 または λ＝5 である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の固有値の言及

【積分方程式】より

…　(1)の核に助変数λを含ませた方程式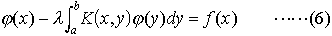，を考えることが多い。この右辺を0で置き換えた方程式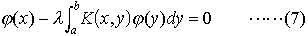，については，φ₀(x)≡0なるφ₀は一つの解であるが，(7)がこのφ₀以外の解φをもつようなλを固有値といい，そのときの解φを固有値λに属する固有関数という。　K(x,y)が実数値で，かつK(x,y)＝K(y,x)を満たすとき，これを対称核という。…

【量子力学】より

…どんな関数がこの性質をもつかは演算子によって違うが，非常に限られた種類のものであることは確かなので，それらを一括して演算子の固有関数とよぶ。そしてを作用させたときの倍率E_nを固有値とよぶ。前項に述べたことと併せていえば，量子力学的な系のエネルギーがとりうる値は，この系のハミルトニアン演算子の固有値に限られる。…

※「固有値」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」