積分方程式（読み）セキブンホウテイシキ（英語表記）integral equation

デジタル大辞泉

せきぶん‐ほうていしき〔‐ハウテイシキ〕【積分方程式】

積分の中に未知の関数を含む方程式。

出典　小学館

精選版 日本国語大辞典

せきぶん‐ほうていしき‥ハウテイシキ【積分方程式】

1. 〘 名詞 〙 関数方程式の一つ。積分の中に未知関数を含む方程式をいう。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

積分方程式 (せきぶんほうていしき)
integral equation

未知関数の積分を含む方程式をいう。1823年にN.H.アーベルが，重力場である曲線Cに沿って落下する質点の，落下時間とCの形との関係を論じて，次の方程式を立てた。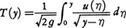

ただし，曲線Cの方程式をx＝φ（y）とするとき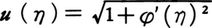，であり，T（y）は高さyから0までの落下時間，gは重力による加速度である。ここで，T（y）を与えてu（η）を求める（それによって曲線Cを定める）問題を考え，上の積分方程式の解として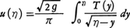，を得た。これが積分方程式の始まりである。しかし積分方程式を系統的に論じたのは，ボルテラV.Volterra（1860-1940）とフレドホルムE.I.Fredholm（1866-1927）である。

　一般的な形として，f（x），K（x，y）を既知関数，φ（x）を未知関数とするとき，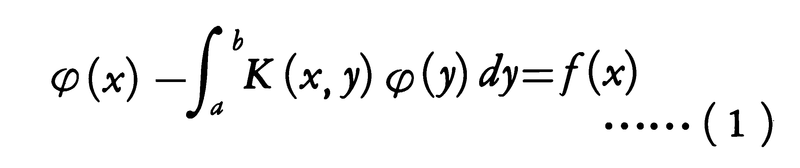



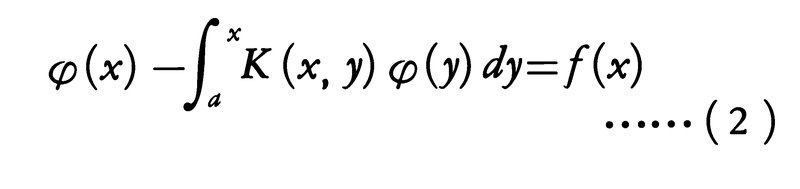
はそれぞれフレドホルム型積分方程式，ボルテラ型積分方程式と呼ばれ，K（x，y）をこれらの方程式の核という。K¹（x，y）＝K（x，y）とおき，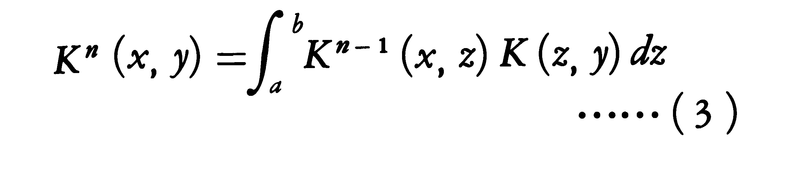

n＞1で定義したKⁿ（x，y）を反復核という。このとき，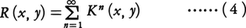

の右辺が一様収束すれば，（1）の解は，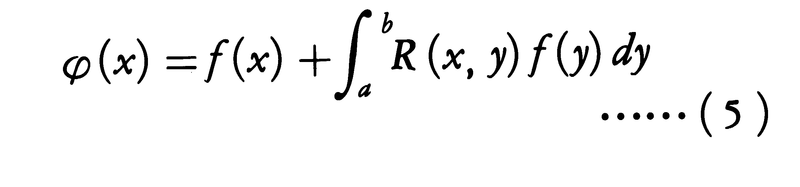

で与えられる。このようなR（x，y）をK（x，y）の解核という。方程式（2）の場合は，（3）の積分区間（a，b）を（y，x）として反復核を定義すれば，（4）の右辺は一様収束して解核R（x，y）が得られ，（5）の積分区間（a，b）を（a，x）とした式により（2）の解が得られる。

　（1）の核に助変数λを含ませた方程式，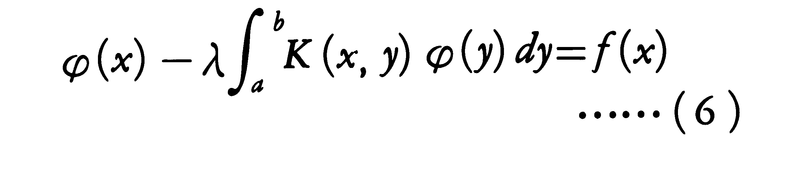

を考えることが多い。この右辺を0で置き換えた方程式，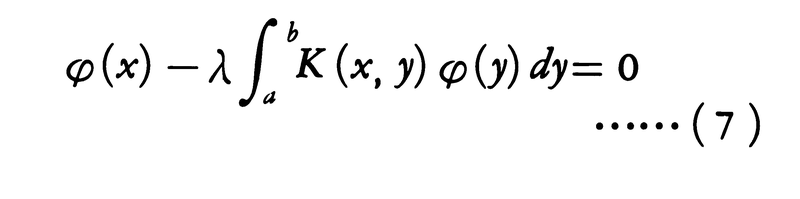

については，φ₀（x）≡0なるφ₀は一つの解であるが，（7）がこのφ₀以外の解φをもつようなλを固有値といい，そのときの解φを固有値λに属する固有関数という。

　K（x，y）が実数値で，かつK（x，y）＝K（y，x）を満たすとき，これを対称核という。K（x，y）が二次元の閉区間a≦x≦b，a≦y≦bで連続な対称核であるとき，次の性質をもつ固有値と固有関数の列｛λ_n｝，｛φ_n｝が存在する。

（1）各nに対しφ_nはλ_nに属する固有関数。

（2）｛｜λ_n｜｝は単調増加で，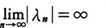


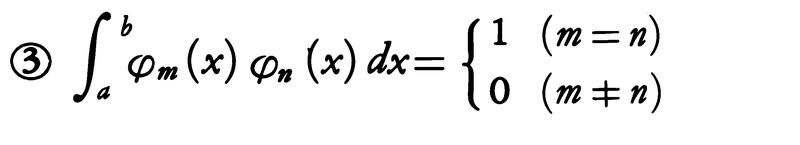
このことを｛φ_n｝は正規直交系をなすという。

（4）任意の固有値λはあるλ_nに等しく，λに属する固有関数はλ＝λ_nなるλ_nに対応するφ_nの線形結合で表される。

　またこのとき，h（x）を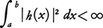，なる関数とすると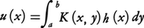，と表される関数u（x）は，正規直交系｛φ_n｝を用いて次の一様収束級数に展開され，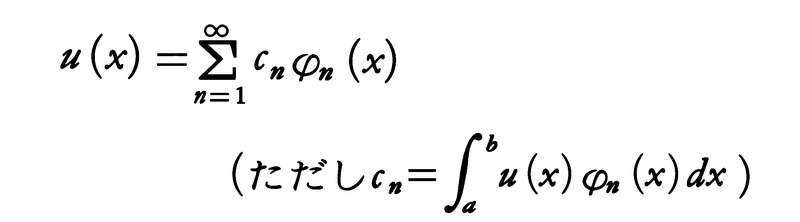

これをヒルベルト=シュミットの展開定理という。λが固有値でないときは（6）の解は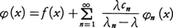，で与えられる。ただしc_nは上に述べたとおりとする。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

積分方程式
せきぶんほうていしき

未知関数の積分を含む関係式を積分方程式という。たとえば、xを独立変数、u(x)を未知関数、f(x),K(x.ξ)を既知関数、λをパラメーターとして関係式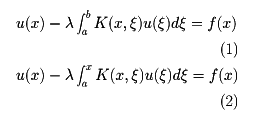

は積分方程式である。（1）をフレドホルム型、（2）をボルテラ型という。独立変数が二つ以上の場合も同様である。

　常微分方程式y″+λy=f(x)の境界条件y(a)=y(b)=0を満たす解y=y(x)を求める問題は、u(x)=y″(x)と置くことにより、（1）の形の積分方程式を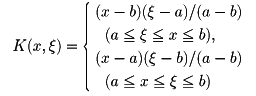

として解くことに同等になる。同様に、常微分方程式の初期値問題はボルテラ型の積分方程式を解くことに同等になる。関数u(x)に関数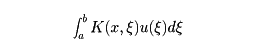

を対応させる作用素をTと書くと、（2）は適当な関数空間における方程式
　　u+λTu=f　　（1）′
の形に書くことができる。この方程式（1）′は連立一次方程式と類似の性質をもつ。これらの性質はバナッハ空間やヒルベルト空間における有界作用素の性質として詳しく調べられている。この結果を用いて、積分方程式、したがって微分方程式の境界値問題などの可解性を論ずることができる。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

積分方程式
せきぶんほうていしき
integral equation

被積分関数のなかに未知関数が含まれている形の方程式，特に積分変換の逆問題の形の方程式。たとえば，f(x) ，K(x，y) を既知関数， を未知関数とすれば，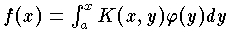



は積分方程式である。関数 K(x，y) を積分方程式の核，積分方程式を満足する関数 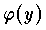をその解という。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

積分方程式【せきぶんほうていしき】

積分記号の中に未知関数を含む方程式。最もよく現れるのは，K（x，y），f（x）を既知関数とし，u（x）を未知関数とするとき（式１）（式２）の形の方程式で，（１），（２）をそれぞれ第一種，第二種のフレドホルムの積分方程式という。→積分
→関連項目解析学

出典　株式会社平凡社