ジョルダン測度（読み）ジョルダンそくど（その他表記）Jordan measure

ブリタニカ国際大百科事典 小項目事典

ジョルダン測度
ジョルダンそくど
Jordan measure

C.ジョルダンは，リーマン積分 (→定積分 ) の考え方をもとにして，点集合の測度を定義した。ここで測度とは，直線上の点集合の長さ，平面上の点集合の面積，空間内の点集合の体積などを拡張した概念をさし，一般の m 次元空間における点集合の容積とでもいうべきものである。このジョルダンの測度を拡度ということもある。以下2次元の場合について述べる。平面上に有界な点集合 A が与えられているとき，各辺が座標軸に平行で1辺の長さが r の正方形の網 Δ をつくり，A をおおう。正方形の中で，A に含まれてしまうものの面積の総和を S_Δ とし，A と少くとも1点を共有するものの面積の総和を S^'_Δ とすると S_Δ＜S^'_Δ となる。ここで網の目を次第に細かく分割して，正方形の1辺の長さ r を0に収束させたとき，それぞれの極限値を
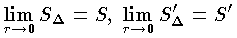とすれば，S≦S′ である。このときの S を A のジョルダン内測度，S′ を A のジョルダン外測度という。特に等号が成り立つ場合 S＝S′ をジョルダン測度という。 A について S＝S′ が確定する場合，この A をジョルダン可測という。

出典　ブリタニカ国際大百科事典 小項目事典