メネラウスの定理 (メネラウスのていり)
Menelaus' theorem
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
メネラウスの定理
めねらうすのていり
三角形ABCにおいて頂点を通らない直線が三辺BC、CA、ABあるいはその延長と交わる点を、それぞれD、E、Fとするとき、各辺を内分あるいは外分する三つの比の積は1となる。すなわち
BD/DC・CE/EA・AF/FB=1
である。これをメネラウスの定理という。メネラウスMenelaus(生没年不詳)は100年ころアレクサンドリアで活躍した天文学者で、球面三角形についての類似の定理をも導いている。この定理の逆も成立する。すなわち、三角形ABCの辺BCの延長上に点Dが、辺CA、AB上に点E、Fがあり、前述の三つの比の積が1ならば、3点D、E、Fは一直線上にある。これは、3点とも辺の延長上にある場合も同様である。これらの定理は、3点が一直線上にあることを証明するのに用いられる。3点が一直線上にある定理を共線定理という。メネラウスの定理の逆の成立は共線定理の基本である。
[柴田敏男]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
メネラウスの定理
メネラウスのていり
Menelaus' theorem
三角形 ABCの3辺 BC,CA,ABまたはその延長が1直線と交わる点をそれぞれP,Q,Rとすれば BP/PC・CQ/QA・AR/RB=1 であるという定理をメネラウスの定理という。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
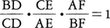 が成り立つことである。
が成り立つことである。


