モソッティ-クラウジウスの式（読み）モソッティクラウジウスノシキ

化学辞典 第2版 の解説

モソッティ-クラウジウスの式
モソッティクラウジウスノシキ
Mossotti-Clausius' equation

クラウジウス-モソッティの式ともいう．無極性分子の物質の誘電率εと分子の分極率αを関係づける式．

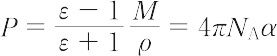
ここで，Pは分子分極，Mは分子量，ρは密度，NA はアボガドロ定数．O.F. Mossotti(1850年)とR. Clausius(クラウジウス)(1879年)により導かれた．εは無次元の数であるから，上式で定義されるPは一種のモル体積であり，多くの場合温度に無関係である．有極性分子に対しては，上式の最右端に分子の配向分極に関する項が付加されたデバイの式となる．

出典　森北出版「化学辞典（第2版）」化学辞典 第2版について　情報

法則の辞典 の解説

モソッティ‐クラウジウスの式【Mossotti-Clausius equation】

「クラウジウス‐モソッティの式」のページをご覧ください。

出典　朝倉書店法則の辞典について　情報

今日のキーワード

初恋

生まれて初めての恋。[補説]書名別項。→初恋[類語]恋・恋愛・愛恋あいれん・愛・恋情れんじょう・恋慕れんぼ・思慕しぼ・眷恋けんれん・色恋いろこい・慕情ぼじょう・恋心・狂恋・悲恋・片恋・片思い・岡惚れ・...

初恋の用語解説を読む