改訂新版 世界大百科事典 「ルレー」の意味・わかりやすい解説
ルレー
Jean Leray
生没年:1906-98
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
…この考えによりG.D.バーコフとケロッグO.D.Kellog(1878‐1932)は,微分方程式の解の存在を,バナッハ空間における(必ずしも線形でない)完全連続作用素の不動点定理として証明した。このような考え方は,シャウダーJ.P.Schauder(1899‐1943),ルレーJ.Leray(1906‐ )らによって,偏微分方程式の解の存在証明にも拡張された。
[線形作用素の半群]
バナッハ空間XからXへの有界線形作用素の族{Tt|t≧0}があって,(a)TtTs=Tt+s(半群性),(b)T0=I(恒等作用素),(c)任意のx∈Xに対して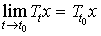 (連続性)を満たすとき,{Tt|t≧0}を1パラメーター半群または単に半群と呼ぶ。…
(連続性)を満たすとき,{Tt|t≧0}を1パラメーター半群または単に半群と呼ぶ。…
…もともとは,1940年代後半に岡潔が多変数関数論の研究の中で,現在の前層にあたるものを利用した。岡はそれを不定域イデアルと呼んだが,他方同じころ,これとは独立にルレーJ.Leray(1906‐ )が同様なものを考えた。その直後,H.カルタンらが層の一般論を展開し,多変数関数論に有効に利用した。…
…この考えによりG.D.バーコフとケロッグO.D.Kellog(1878‐1932)は,微分方程式の解の存在を,バナッハ空間における(必ずしも線形でない)完全連続作用素の不動点定理として証明した。このような考え方は,シャウダーJ.P.Schauder(1899‐1943),ルレーJ.Leray(1906‐ )らによって,偏微分方程式の解の存在証明にも拡張された。
[線形作用素の半群]
バナッハ空間XからXへの有界線形作用素の族{Tt|t≧0}があって,(a)TtTs=Tt+s(半群性),(b)T0=I(恒等作用素),(c)任意のx∈Xに対して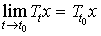 (連続性)を満たすとき,{Tt|t≧0}を1パラメーター半群または単に半群と呼ぶ。…
(連続性)を満たすとき,{Tt|t≧0}を1パラメーター半群または単に半群と呼ぶ。…
…もともとは,1940年代後半に岡潔が多変数関数論の研究の中で,現在の前層にあたるものを利用した。岡はそれを不定域イデアルと呼んだが,他方同じころ,これとは独立にルレーJ.Leray(1906‐ )が同様なものを考えた。その直後,H.カルタンらが層の一般論を展開し,多変数関数論に有効に利用した。…
※「ルレー」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...