関数空間（読み）カンスウクウカン（その他表記）function space

デジタル大辞泉

かんすう‐くうかん〔クワンスウ‐〕【関数空間】

一定の区間で定義された連続性をもつ関数全体の集合。

出典　小学館

精選版 日本国語大辞典

かんすう‐くうかんクヮンスウ‥【関数空間】

1. 〘 名詞 〙 一定の区間で定義された連続関数全体の集合。この集合の元に対して、和、定数倍を次のように定義することができる。(f+ɡ)(x)=f(x)+ɡ(x), (af)(x)= a(f(x))。また、多変数関数を元とするものも考えられる。さらに、より一般化して一つの集合から他の集合へのある種の写像全体の集合をいうこともある。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

関数空間 (かんすうくうかん)
function space

関数f（x）を微分するという演算はf（x）にその導関数f′（x）を対応させることであり，また0≦y≦x≦1なる2変数（x，y）の関数K（x，y）が与えられたとき，区間［0，1］の上の関数fに対して，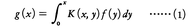

なる関数gを対応させると，これも関数から関数への対応（写像）である。このように，微分・積分などの演算を含む関数から関数への対応を統一的に扱うのが，現代の解析学の一つの重要な特徴である。そのために，ある条件をみたす関数の全体を一つの集合と考え，個々の関数をその集合の要素として扱うとき，その集合を関数空間という。通常，関数空間においては距離を定義して収束を考える。このような研究方法は，20世紀に入ってから，フレッシェM.Fréchet，リースF.Rieszらによって始められたものである。以下に重要な関数空間の例を挙げる。

（1）C：区間［0，1］で定義された連続関数f（x）の全体をCとし，f，g∈Cに対して，距離を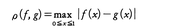，と定義する。はf_n（x）がf（x）に区間［0，1］の上で一様収束することである。

（2）C^r：区間［0，1］上で連続なr階導関数をもつ関数の全体をC^rとし，f，g∈C^rに対して距離をf⁽⁰⁾（x）＝f（x）として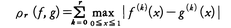，と定義する。初めに例にあげたf→f′なる写像は，C¹からCへの連続写像である。

（3）L_p（p≧1）：区間（0，1）で定義された可測関数fで，｜f（x）｜^pがルベーグ積分可能であるものの全体をL_pとし，距離を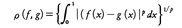，と定義する。

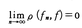のとき，関数f_nが関数fに（p次）平均収束するという。（1）式においてK（x，y）が有界可測関数ならば，（1）式で定義される写像f→gはL_pからL_pの中への連続写像である。p＝2のとき，すなわちL₂においては内積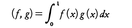，が定義され，L₂はヒルベルト空間になる。

　このほかにも，いろいろの関数空間が考えられ，それらに関して，偏微分方程式などに応用されるすぐれた理論が構成されて，現在も盛んに発展しつつある。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

関数空間
かんすうくうかん
functional space

関数のなす集合に，代数的演算や位相を導入した空間。変分法で，関数 f に対して定まる汎関数 I(f) の極大を論じようとするときなど，f を元とする空間 Ω でのワイエルシュトラスの定理を問題にしなければならなくなる。いま，1変数あるいは n 変数の，実数値あるいは複素数値連続関数全体の集合を Ω とする。ここで Ω に位相を与えれば，Ω は位相空間になる。こうしてできた位相空間の元は関数であるから，Ω は関数空間と呼ばれる。このような関数の集合 Ω に位相を与える方法はいろいろあるが，一般には，Ω が距離空間になるように位相を導入する。たとえば，閉区間 [0，1] で定義された連続関数全体の集合を Ω とするとき，Ω の任意の 2元 f(x)，g(x)(x∈[0，1]) の距離を ｜f(x)－g(x)｜ の上限，すなわち ρ(f，g)＝ sup ｜f(x)－g(x)｜ と定義すれば，Ω は距離ρについての距離空間となる。したがって Ω は位相空間となり，それゆえ関数空間である。また関数空間は，位相空間であるとともに，ベクトル空間ともなる。それには Ω の任意の 2元 f，g に対して，ベクトル空間の基本演算である和 f＋g および f の a 倍 (a はスカラー) を，自然に定義すればよい。関数空間の理論は，現代解析学の多くの問題を位相数学の応用として，統一的に取扱うための一般的な手段である。関数空間の研究に基本的な意味をもつ空間に，ヒルベルト空間やバナッハ空間がある。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

関数空間
かんすうくうかん

閉区間［a, b］上の連続関数全体の集合をC［a, b］で表すと、C［a, b］は普通の和や定数倍に関しベクトル空間になる。さらにfのノルムを‖f‖で表し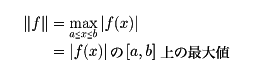

により定義すると、ノルムは絶対値と同様な性質を満たす。‖f－g‖により、C［a, b］の2点f、gの距離を定義すると、C［a, b］はこの距離により距離空間となり、しかも完備になる。したがって、C［a, b］はバナッハ空間となり、関数解析が使える。このように、関数が要素となるノルムの定義されたベクトル空間を関数空間という。

　C［a, b］のほかに、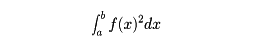

が（ルベーグ積分の意味で）有限になる関数の全体をL²(a, b)で表すと、この要素f、gに、内積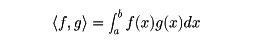

が定義されて、ヒルベルト空間になる。

［洲之内治男］

出典　小学館　日本大百科全書(ニッポニカ)