多変数関数論（読み）たへんすうかんすうろん（その他表記）theory of function of many variables

改訂新版　世界大百科事典

多変数関数論 (たへんすうかんすうろん)
theory of function of many variables

関数論の中で，二つ以上の独立変数をもつ関数を対象とする分野である。

　複素n次元空間Cⁿ（n≧2）の領域Dで定義された複素数値関数，

　w＝f（z₁，z₂，……，z_n）

は，もし各点（a₁，a₂，……，a_n）∈Dで複素偏微分可能のとき，すなわち次のことが成り立つとき，Dで正則であるという。各k＝1，2，……，nに対し，f（a₁，……，a_k-1，z_k，a_k+1，……，a_n）がz_kの関数としてa_kの近傍で（一変数）正則関数である。

　以上の意味で正則な関数は，Dで連続である（ハルトークスの定理Hartogs' theorem）。このことは偏微分可能な実関数の場合との著しい相違である。

　D_kが複素平面の領域で，なめらかな曲線C_kで囲まれているとき，Cⁿの領域D＝｛（z₁，……，z_n）｜z_k∈D_k，k＝1，……，n｝に対して，次のコーシー積分公式が成り立つ。すなわち，fがDの閉包を含む領域で正則なとき，任意の（z₁，……，z_n）∈Dに対して，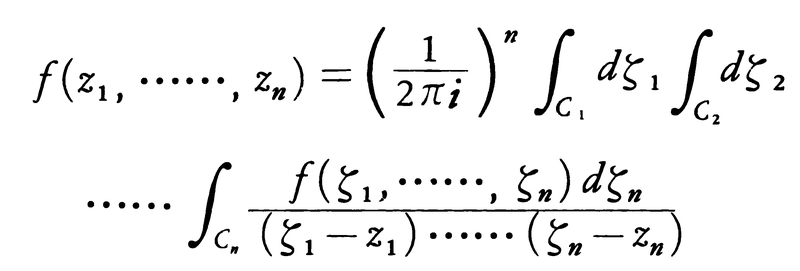

となる。

　多変数べき級数は，その中心の近傍で正則である。逆に，正則な関数は，各点を中心として，べき級数に展開できる。

　多変数正則関数に対しては，次の形の一致の定理が成り立つ。領域D⊂Cⁿの正則関数fとgが，もしある開集合で一致するならば，Dで一致する。この一致の定理に基づいて，解析接続という概念は，一変数関数とまったく同様に定義することができる。

　n＝2のとき，領域D＝｛（z₁，z₂）｜｜z₁｜＜1，｜z₂｜＜1｝－｛（z₁，z₂）｜｜z₁｜≦1/2，｜z₂｜≦1/2｝は，次の性質をもっている。Dの正則関数は，すべて領域｛（z₁，z₂）｜｜z₁｜＜1，｜z₂｜＜1｝の正則関数に解析接続される。n≧3でも，同じような例が作られる。これらのことは，多変数正則関数が一変数正則関数とは際だって異なる性質をもつということを示している。実際，一変数の場合は，任意の領域に対し，その境界を自然境界とする（つまり，より広い領域への解析接続が不可能な）正則関数が存在するからである。

　境界が，ある正則関数の自然境界となっている領域を正則領域という。また，そのような領域は正則凸であるともいう。このようなものの研究は，多変数関数論の重要な1章である。研究手段にも，通常の関数論的な方法のほかに，層のコホモロジー理論などの代数的方法も用いられ，内容，方法とも，一変数関数論とは大きく異なっている。

　歴史的には，多変数関数論の起源は19世紀中期のアーベル関数の研究にあるということができ，K.ワイヤーシュトラスの仕事に代表される。20世紀に入り，ハルトークスF.Hartogsによって，前述のような，一変数関数との相違が明確にされて以来，独自の発展を始めた。1930年代以降，正則領域が多くの者の研究対象になったが，その中にあって，日本の岡潔の貢献はきわめて大きい。そのほかには，C.ジーゲルの多変数保型関数の研究が重要である。現在は，代数幾何，多様体，偏微分方程式などの各分野とのかかわりも深い。
執筆者：及川 廣太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」