一次分数変換（読み）いちじぶんすうへんかん（英語表記）linear fractional transformation

改訂新版　世界大百科事典

一次分数変換 (いちじぶんすうへんかん)
linear fractional transformation

メービウス変換Möbius transformationともいう。定数a，b，c，dが複素数で，ad－bc≠0であるとき関数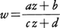を一次分数関数といい，これより定まる写像を一次分数変換という。これはc≠0のとき－\(\frac{d}{c}\)以外の複素平面C上で定義され，c＝0のときは複素平面C上で定義される。a:b:c:dが一定であれば同じ関数を表すから，ad－bc＝1と仮定しても一般性を失わない。c≠0のときはこの一次分数関数はC－｛－\(\frac{d}{c}\)｝からC－｛\(\frac{a}{c}\)｝への1対1上への写像を与え，逆写像は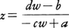で与えられる。c＝0のときはCからCへの1対1上への写像を与える。c≠0のときzを－\(\frac{d}{c}\)に近づけると対応するwの絶対値は無限大に発散する。またzの絶対値が無限大に発散するときwの値は\(\frac{a}{c}\)に近づく。そこでz＝－\(\frac{d}{c}\)の像を∞と定義して無限遠点∞を考えることにし，∞の像を\(\frac{a}{c}\)と定める。c＝0のときは∞の像は∞と定める。このようにして，一次分数関数は複素平面に無限遠点をつけ加えたものからそれ自身への同型写像と考えることができる。この写像を一次分数変換という。逆写像も一次分数変換である。直線は無限遠点を通る円と考えると，一次分数変換は円を円にうつす。また4点z₁，z₂，z₃，z₄の非調和比（z₁，z₂，z₃，z₄）＝（z₁－z₃）/（z₁－z₄）:（z₂－z₃）/（z₂－z₄）は一次分数変換によって変わらない。複素平面に無限遠点をつけ加えたものはリーマン球面と呼ばれる。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」