日本大百科全書(ニッポニカ) 「非調和比」の意味・わかりやすい解説
非調和比
ひちょうわひ
non-harmonic ratio
1直線上にA、C、B、Dの順番に並ぶ4点A、B、C、Dがあるとき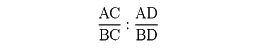
を4点の非調和比または複比といい、これを(AB,CD)で表す。ここでACはA、C間の符号をもった長さである。したがって、この直線上に座標を導入して、4点の座標をそれぞれx1、x2、x3、x4とすれば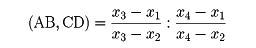
となる。また1平面上にあるA、B、C、Dを通る4直線a、b、c、dが1点Oで交わるとき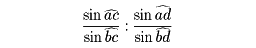
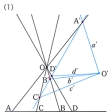
を4直線の非調和比といい(ab,cd)と表す。ここで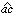 は直線a、cがなす符号をもつ角とする。非調和比は射影変換によって値が変わらないというおもしろい性質をもっているが、それはの(1)で
は直線a、cがなす符号をもつ角とする。非調和比は射影変換によって値が変わらないというおもしろい性質をもっているが、それはの(1)で
(AB,CD)=(ab,cd)
=(A′B′,C′D′)
=(a′b′,c′d′)
が成り立つためである。航空写真をとったとき、地上にある1直線上の4地点と印画紙上に写された4点の非調和比は等しいので、地上の3地点相互間の距離がわかっていれば、非調和比を利用して第4の地点までの距離を知ることができる。非調和比の値が-1であるような4点を調和列点、4直線を調和線束という。円周上の4点の非調和比は、これらと異なる任意の点Pを円周上にとり、の(2)の4直線a、b、c、dの非調和比として、すなわち、(AB,CD)=(ab,cd)として定義する。このように定義された(AB,CD)は円周上の点Pの位置に関係なく一定の値をもつことが容易にわかる。直線上の4点の非調和比は射影対応で不変であるから射影幾何学で、また円周上の4点の非調和比は反転で不変であるから共形幾何学で基本的な役割をする。
[立花俊一]


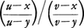 の値は
の値は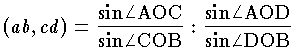 となる。非調和比は,射影変換によって不変である。
となる。非調和比は,射影変換によって不変である。
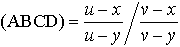 は座標のとり方によらない数で,4点A,B,C,Dの非調和比と呼ばれる。4点の中に無限遠点l∞があるときも,例えば(ABCl∞)=(u-x)/(u-y)のように定義される。…
は座標のとり方によらない数で,4点A,B,C,Dの非調和比と呼ばれる。4点の中に無限遠点l∞があるときも,例えば(ABCl∞)=(u-x)/(u-y)のように定義される。…