無限遠点（読み）むげんえんてん（その他表記）point at infinity

改訂新版　世界大百科事典

無限遠点 (むげんえんてん)
point at infinity

平面は閉じていないが，1点をつけ加えたり，または平面の各方向にそれぞれ1点をつけ加えれば，平面は閉じた面となる。このときつけ加えられる新しい点を無限遠点という。二つの場合に分けてもう少し詳しく説明しよう。

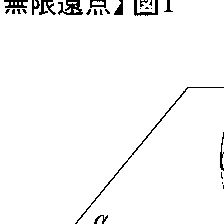
　（1）平面αが与えられたとき，その上に中心Oをもつ球面Sをつくり，αに垂直な直径の一端をNとして，α上の各点Qに対し直線NQとSとの交点Pを対応させる（図1）。この対応によりα上の点とNを除いたS上の点とは1対1に対応する。Nに応ずるα上の点はないが，PがNに近づくとき，QはOからどんどん遠くへ離れていく。そこでα上の無限の遠くに新しい1点をつくり，この点がNに対応するとすれば，この点も含めたαはSと同一視でき，閉じた面となる。新しい1点を∞で表し，無限遠点という。複素平面に∞を導入すれば，例えば複素数zを1/zにうつす関数なども1対1となり複素関数の研究に便利である。

　（2）平面αに接する球面Sをつくり，接点をT，球の中心をO，αに平行なSの大円をCとする。いま，α上の各点Qに対し，直線OQとSとの交点をP，P^＊とすれば，これらは対心点で，Qを｛P，P^＊｝にうつす対応によりα上の点とCに含まれないS上の対心点の組とは1対1に対応する。Cに含まれる対心点の組に応ずるα上の点はないが，｛P，P^＊｝がTを通る大円に沿ってC上の対心点の組に近づけばQはこの大円の面とαとの交わりである直線上をTからどんどん遠くへ離れていく（図2）。それでTを通る各直線lに対し，その上の無限の遠くに新しい1点l∞をつくり，この点がlと平行なSの直径の両端であるC上の対心点の組に対応するとすれば，すべてのl∞を含めたαはS上の対心点の組全体の集合，したがってS上の対心点のおのおのをはり合わせてできる曲面（これを射影平面という）と同一視でき，閉じた面となる。l∞をlの方向の無限遠点と呼び，すべての方向の無限遠点は新しい一つの直線をつくると考えて，これを無限遠直線と呼ぶ。平面上の平行な2直線はその方向の無限遠点で交わると考えれば，平面上の相異なる2直線はつねに1点で交わることになり，点や直線の結合的性質が統一的に研究でき便利である。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

無限遠点
むげんえんてん

「無限遠直線」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の無限遠点の言及

【関数論】より

…これをfの因数分解という。例えば，
［無限遠点］
　複素平面に，新たに1点をつけ加えてとおく。つけ加えられた点を無限遠点と呼び，記号∞で表す。…

【射影幾何学】より

…このような例外を解消するため次のように考える。空間の各直線lに対し，無限遠点と呼ぶ1点l_∞を想像し，直線l,l′が平行ならばl_∞＝l′_∞，そうでなければl_∞≠l′_∞と約束する。そして，平面αにその上の直線に対する無限遠点をすべてつけ加えて，これをで表し，上にある無限遠点全体で一つの直線(無限遠直線)をつくると考える。…

※「無限遠点」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」