交項級数（読み）こうこうきゅうすう（英語表記）alternating series

改訂新版　世界大百科事典

交項級数 (こうこうきゅうすう)
alternating series

a₁，a₂，……，a_n，……がすべて≧0であるとき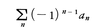，の形の級数を交項級数という。すなわち，交項級数とはa₁－a₂＋a₃－a₄＋……の形に，正の項と負の項が交互に現れる級数であって，交代級数とも呼ばれる。数列｛a_n｝が単調減少で，n→∞のときa_n→0となるならば，

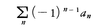は収束する。これをライプニッツの定理という。たとえば，級数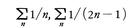，は発散するが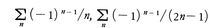，は収束する。これらの級数の和は，それぞれlog2，π/4となることが知られている。なお，次の例も有名である。｜x｜＜πならば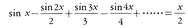，　ライプニッツの定理は広義積分の収束の証明にも応用される。たとえば，積分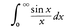，は，区間（n－1）π＜x≦nπにおける積分を第n項とする交項級数となって，収束する。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

交項級数
こうこうきゅうすう

「交代級数」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典