関連語
精選版 日本国語大辞典 「偏導関数」の意味・読み・例文・類語
へん‐どうかんすう‥ダウクヮンスウ【偏導関数】
ブリタニカ国際大百科事典 小項目事典 「偏導関数」の意味・わかりやすい解説
偏導関数
へんどうかんすう
partial derivative
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
日本大百科全書(ニッポニカ) 「偏導関数」の意味・わかりやすい解説
偏導関数
へんどうかんすう
partial derivative
多変数の関数に対し、そのうちの一つの変数について微分して得られる導関数。
いま、二変数の関数について述べると、関数z=f(x,y)で、yは固定してxのみの関数と考え、xについて微分する。このようにすることをf(x,y)をxについて(偏)微分するといい、その導関数をf(x,y)のxに関する偏導関数とよんで、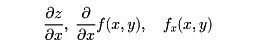
などで表す。yに関する偏導関数も、同じように定められる。
たとえば、f(x,y)=x2+y2とするとき、
fx(x,y)=2x, fy(x,y)=2y
[竹之内脩]
世界大百科事典(旧版)内の偏導関数の言及
【微分】より
…簡単のために2変数の関数f(x,y)について書くと,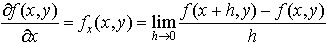 によってfのxに関する偏微分係数が定義される。この偏微分係数をx,yの関数と考えるとき,その関数をfのxに関する偏導関数という。偏微分係数,または偏導関数を求める手続きを偏微分法という。…
によってfのxに関する偏微分係数が定義される。この偏微分係数をx,yの関数と考えるとき,その関数をfのxに関する偏導関数という。偏微分係数,または偏導関数を求める手続きを偏微分法という。…
【偏微分】より
…例えば2変数の関数f(x,y)について書くと,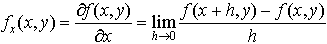 がfのxに関する偏微分係数である。これをx,yの関数と考えるときfのxに関する偏導関数という。偏微分係数,あるいは偏導関数を求める手続を偏微分法というが,この偏微分法のことを偏微分と略称することが多い。…
がfのxに関する偏微分係数である。これをx,yの関数と考えるときfのxに関する偏導関数という。偏微分係数,あるいは偏導関数を求める手続を偏微分法というが,この偏微分法のことを偏微分と略称することが多い。…
※「偏導関数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


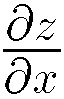 、yについての偏導関数を
、yについての偏導関数を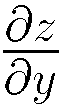 で表わす。
で表わす。