日本大百科全書(ニッポニカ) 「円周等分多項式」の意味・わかりやすい解説
円周等分多項式
えんしゅうとうぶんたこうしき
多項式xn-1を整数係数の既約因数に分解したとき現れる既約多項式をいう。たとえばx3-1=(x-1)(x2+x+1)の既約因数x-1、x2+x+1などを円周等分多項式という。多項式xn-1はn個の複素数
cos(2kπ/n)+isin(2kπ/n) (k=1,2,…,n)
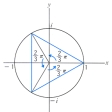
を根(こん)にもつが、これらn個の複素数はn乗すると1になり、1のn乗根といわれる。これらを複素平面(ガウス平面)の点で表すと、原点を中心とした単位円の円周を1を起点としてn等分する点になり、それらを次々に直線で結ぶと、単位円に内接する正n角形ができる。これが円周等分多項式という名前のおこりである。たとえば1の3乗根は
cos(2kπ/3)+isin(2kπ/3)
であり、これをk=1,2,3について計算したもの
をつなぐとのような正三角形となる。
1のn乗根のうち
ε=cos(2π/n)+isin(2π/n)
のべきε1,ε2,ε3,……を順につくっていくと、n乗して初めて1になる。このようにn乗して初めて1になる複素数を、1の原始n乗根という。たとえば、1の6乗根は、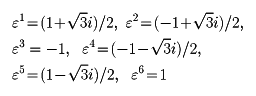
の六つであるが、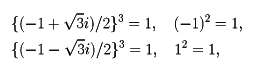
であるから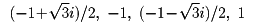
は原始6乗根ではない。
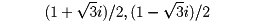
は6乗して初めて1になるから原始6乗根である。1のn乗根
εk=cos(2πk/n)+isin(2πk/n)
が1の原始n乗根になるための必要十分条件は、kとnが互いに素であることである。1の原始6乗根ε1、ε5は、因数分解
x6-1=(x-1)(x+1)(x2+x+1)(x2-x+1)
の既約因数x2-x+1の根として求められる。このように、1の原始n乗根は、多項式xn-1を因数分解したときのある既約因数の根である。この多項式を円周n等分多項式という。たとえば、円周六等分多項式はx2-x+1である。
[菅野恒雄]