因数分解（読み）インスウブンカイ（英語表記）factorization

デジタル大辞泉

いんすう‐ぶんかい【因数分解】

［名］(スル)数や整式を因数の積の形に直すこと。例えば、21を3×7と素因数分解したり、a²－b²を（a＋b）（a－b）としたりすること。

出典　小学館

精選版 日本国語大辞典

いんすう‐ぶんかい【因数分解】

1. 〘 名詞 〙 整数または整式を、いくつかの整数または整式の積の形に表わすこと。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

因数分解 (いんすうぶんかい)
factorization

一つの整数あるいは多項式を，いくつかの整数あるいは多項式の積の形に変形すること。例えば整数60は2²×3×5に，多項式x²＋5x＋6は（x＋2）（x＋3）に因数分解される。自然数nが1とn以外の約数をもてば，必ず\(\sqrt{n}\)以下の約数をもつから，nを素因数分解するためには，\(\sqrt{n}\)以下の素数pについてpがnの約数になるかどうかを調べればよい。

　以下では，多項式の因数分解について考える。有理数係数の多項式が与えられたとき，ふつうは各因数を有理数係数の多項式の範囲で考えて，それ以上分解できないところまで分解する。しかし目的によってはもとの多項式の係数よりも，因数の係数の範囲を拡張して，例えば有理数係数の多項式を複素数係数の多項式へ因数分解することもある。

　有理数係数の多項式を因数分解した結果を書き表すときは，見た目がきれいであるように書くのが原則である。例えば，x²＋5/6x＋1/6＝1/6（2x＋1）（3x＋1），4x²＋14x＋12＝2（2x＋3）（x＋2）のように，（1）一つのかっこの中は，ある文字について次数の順に並べ，（2）定数因数は最初にまとめてくくり出し，それぞれのかっこの中は各係数が整数で，係数の最大公約数が1であるように表すのがふつうである。

　積の形をした式を単項式の和の形に変形することは因数分解の逆で，展開するという。展開することは掛算を実行すればよいのであるから容易である。しかし，与えられた多項式を因数分解することは，一般には困難であり，因数分解を求めるための一般的法則は存在しない。比較的簡単な多項式については，次のような方針が役だつことがある。まず，いくつかの文字を含む多項式については，いちばん次数の低い文字について，次数の順に整理する。次に，いくつかの項に共通している因子をかっこの外にくくり出す。例えば，

　a²－ab－ac＋bc＝（－a＋b）c＋a²－ab

　　＝（－a＋b）c＋a（a－b）

　　＝（－a＋b）（c－a）＝（a－b）（a－c）

　上の変形では，最初にcについて一次の項，0次の項ごとにまとめ，次に共通の因子a，次いで（－a＋b）をかっこの外にくくり出して整理した。

　特別な形の多項式については，公式を作って記憶しておき，その公式にあてはめて因数分解を行う。因数分解の公式としては次のものがある。

　a²±2ab＋b²＝（a±b）²　………（1）　

　a²－b²＝（a＋b）（a－b）　……（2）　

　x²＋（a＋b）x＋ab＝（x＋a）（x＋b）　…………（3）　

　acx²＋（ad＋bc）x＋bd＝（ax＋b）（cx＋d）　…………（4）　

　a³±3a²b＋3ab²±b³＝（a±b）³　…………………（5）　

　a²＋b²＋c²＋2ab＋2bc＋2ca＝（a＋b＋c）²　……………（6）　

　a³＋b³＋c³－3abc＝（a＋b＋c）（a²＋b²＋c²－ab－bc－ca）　……（7）　

上の公式を実際に適用するためにはいろいろなくふうが必要である。例えば，

　x⁴＋4＝x⁴＋4x²＋4－4x²

　　　 ＝（x²＋2）²－（2x）²

　　　 ＝（x²＋2x＋2）（x²－2x＋2）

この例では，もとの多項式に含まれていない項4x²をつけ加えて，平方の差の形に変形したのち，公式（2）を適用したのである。

　1変数の多項式f（x）は，f（α）＝0となるとき，かつそのときに限りx－αを因数としてもつ。これを因数定理と呼ぶ。f（x）＝0の根αが，なにかの方法でわかれば，f（x）をx－αで割って，f（x）＝（x－α）g（x）と分解できる。とくに整数係数の多項式f（x）＝a₀xⁿ＋a₁xⁿ⁻¹＋……＋a_nについて，αが有理数であるような一次因数x－αをもてば，αは（±a_nの約数）/（a₀の約数）と表されるという事実は有用である。例えば，f（x）＝x³－6x²＋11x－6について，6の約数α＝1，2，3，6について，各f（α）を計算すれば，f（1）＝f（2）＝f（3）＝0であるから，f（x）＝（x－1）（x－2）（x－3）という分解を得る。また四次以下の多項式については根の公式を利用することもできる。2個以上の文字，例えばx，y，zを含む多項式g（x，y，z）についても，xを変数と考えて，因数定理を適用することができる。g（x，y，z）＝x³＋x²z－x²y＋xy－xyz－y²で，xにyを代入すると，g（x，y，z）＝y³＋y²z－y³＋y²－y²z－y²＝0となる。したがって，g（x，y，z）はx－yを因数にもち，g（x，y，z）＝（x－y）（x²＋zx＋y）と分解される。

　特別な形をした多項式に対しては，対称式，交代式などの性質が用いられる。任意の交代多項式は，差積と対称多項式の積として表される。例えば，

　x³y－x³z－y³x＋y³z＋xz³－yz³＝（x＋y＋z）（x－y）（x－z）（y－z）

したがって，交代式の因数分解は，対称式の因数分解に帰着される。対称式の因数は対称式である。例えば，

　x²y＋x²z＋xy²＋y²z＋xz²＋yz²＋3xyz＝（x＋y＋z）（xy＋yz＋zx）
執筆者：杉江 徹

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

因数分解
いんすうぶんかい

一つの整式が二つ以上の整式の積に等しいとき、積に現れる各整式をもとの整式の因数といい、与えられた整式をその因数の積で表すことを因数分解するという。たとえば、
　 2x³＋4x＝2x(x²＋2)
　　a²－b²＝(a－b)(a＋b)
における右辺が左辺の因数分解である。因数が数または文字であるとき、それを数因数あるいは文字因数という。また与えられた式の各項に共通な因数を共通因数という。前記の第一の例で、2は数因数、xは文字因数であり、これらはまた共通因数でもある。

　一般に因数分解はできるだけ（各因数がそれ以上因数分解できないまで）分解することが普通である。たとえば前掲の第二の例で二つの因数a－b、a＋bはもはや因数分解できない。また第一の例で因数x²＋2は、係数を実数に制限すれば、もはや分解できない。しかし係数に複素数を許せば、これはさらに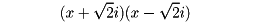

と分解される。したがって、どこまで分解可能かは、式そのものと、係数の許容範囲に依存する。因数分解の正しい指示としては、係数の許容範囲を明示すべきであるが、その指示がないときは、慣行として係数の範囲を実数域とする。

　任意の整式を因数分解する一般的方法は存在しない。与えられた式に即して分解の方法がくふうされる。しかし、基本的な因数分解の公式が応用される。たとえば、公式a²－b²＝(a－b)(a＋b)を用いて、
　 9x²－4y⁴＝(3x)²－(2y²)²
　　　　　＝(3x－2y²)(3x＋2y²)
と分解される。また公式a²＋2ab＋b²＝(a＋b)²を用いて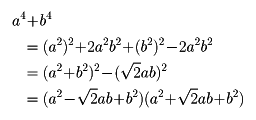

を得る。これらの公式は右辺から左辺を得るとみなせば、いわゆる乗法公式（または展開公式）となる。

　方程式論と関連して、係数を複素数まで許せば、n次代数方程式
a₀xⁿ＋a₁x^n－1＋……＋a_n－1x＋a_n＝0
の根をα₁、α₂、……、α_n（重根を含めて）とすると、
　　a₀xⁿ＋a₁x^n－1＋……＋a_n
　　　＝a₀(x－α₁)(x－α₂)……(x－α_n)
と因数分解される。

［竹内芳男］

因数分解公式

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

因数分解
いんすうぶんかい
factorization

一つの整数あるいは整式（多項式）を，いくつかの整数あるいは整式の積の形に変形することを，その整数あるいは整式を因数分解するという。その積の形をつくっているおのおのの整数あるいは整式を，その積の因数という。たとえば整数 24は 2×2×2×3 に，整式 x³＋3x²＋2x は x(x＋1)(x＋2) に因数分解される。2，3は 24の因数，x，(x＋1)，(x＋2) は x³＋3x²＋2x の因数である。一般に合成数の因数分解は，1通りとはかぎらないが，これを素数の積に分解する方法は 1通りである。整式を因数分解する場合は，普通各因数を整数係数の多項式の範囲で止め，またこの範囲でそれ以上分解できないところまで因数分解するが，実係数もしくは複素係数で行なうこともある。因数分解は，積の展開の逆操作である。因数分解を行なうには基本的な諸公式を組み合わせて適用するのが普通だが，近年特に 1変数多項式については，計算機による数式処理によって有効な算法が開発されている。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

因数分解【いんすうぶんかい】

与えられた数または式をその因数の積として表すこと。たとえばx²−y²＝（x＋y）（x−y）。特に整数を素数の積として表すことを素因数分解という。
→関連項目剰余定理

出典　株式会社平凡社

世界大百科事典（旧版）内の因数分解の言及

【関数論】より

…このとき，整数ν,q_kと正則関数g(z)を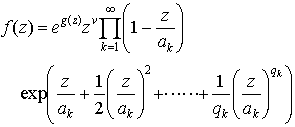，が成り立つようにとることができる。これをfの因数分解という。例えば，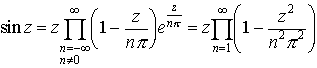
［無限遠点］
　複素平面に，新たに1点をつけ加えてとおく。…

※「因数分解」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」