ガウス平面（読み）ガウスヘイメン

デジタル大辞泉

ガウス‐へいめん【ガウス平面】

直交座標の横軸に実数値、縦軸に虚数値をとり、一つの複素数を一つの点で示す平面。複素平面。数平面。

出典　小学館

精選版 日本国語大辞典

ガウス‐へいめん【ガウス平面】

1. 〘 名詞 〙 ＝ふくそへいめん（複素平面）

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

ガウス平面
がうすへいめん

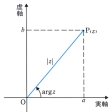
座標平面上の点P(a,b)に、複素数z＝a＋biを対応させると、平面上の点と複素数とが1対1に対応づけられる。このようにして複素数を対応づけて考えた平面をガウス平面、または複素平面という。P(a,b)をP(z)あるいは単にzと表し、x軸を実軸、y軸を虚軸という。実数が直線上の点で表されることの拡張として、複素数を平面上の点で表し、四則演算との関係を図形的に述べたのはガウスである。

　複素数z＝a＋biに対して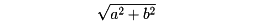

をzの絶対値といい|z|で表す。またz≠0のとき半直線OPと実軸の正の方向とのなす角θをzの偏角といい、argzで表す。普通は、θを－π＜θ≦πまたは0≦θ＜2πに限ることが多い。また、z＝0の偏角は考えない。argはargumentの略である（図A）。複素数z＝a＋bi(≠0)の絶対値|z|をr、偏角argzをθとすると、a＝rcosθ,b＝rsinθとなるので
　　z＝r(cosθ＋isinθ)
と表される。これをzの極形式という。

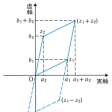
　複素数z₁＝a₁＋b₁i，z₂＝a₂＋b₂iに対して
　　z₁＋z₂＝(a₁＋a₂)＋(b₁＋b₂)i
であるから、z₁＋z₂は原点O、点z₁、点z₂からつくられる平行四辺形の頂点を表す。また点－z₂は点Oに関する点z₂の対称点であるから、点z₁－z₂はO、z₁、－z₂から平行四辺形をつくればよい（図B）。複素数の積と商を考えるときには、極形式を用いる。

　　z₁＝r₁(cosθ₁＋isinθ₁),
　　z₂＝r₂(cosθ₂＋isinθ₂)
とすると、三角関数の加法定理を用いて
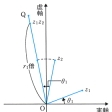
　　z₁z₂＝r₁r₂｛cos(θ₁＋θ₂)＋isin(θ₁＋θ₂)｝
となる。そこでz₁z₂は、絶対値がr₁r₂で、偏角がθ₁＋θ₂であるから、初めの2点z₁、z₂からz₁z₂を作図するには、次のようにすればよい。まず、点z₂を原点の周りにθ₁だけ回転した点Qをとる。次に半直線OQ上に、OQをr₁倍した点をとる。その点がz₁z₂である（図C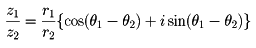）。また、

であるから、点z₁/z₂も、同様に回転と伸縮によって作図することができる。

［寺田文行］

1のn乗根

自然数nに対して、xⁿ＝1を満たす複素数を1のn乗根という。1のn乗根はちょうどn個あって、それらは次のように表される。

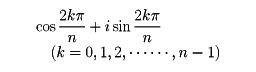
1のn乗根がこのようになることをみるには、ド・モアブルの定理を用いる。xⁿ＝1の解を極形式で表して
　　x＝r(cosθ＋isinθ) (r＞0，0≦θ＜2π)
とすると、ド・モアブルの定理から
　　rⁿ(cosnθ＋isinnθ)＝1
となり、これから絶対値と偏角を考えて
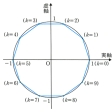
　　rⁿ＝1, nθ＝2kπ
となる。これらをガウス平面上にとると、図Dに示したように、単位円をn等分する点になる。このうちとくにk＝1のときの数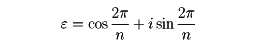

をとると、1のn乗根は
　　1,ε,ε¹,ε²,……,ε^n-1
となり、εを生成要素とする位数nの巡回群であることがわかる。1のn乗根を表すガウス平面上の点を順に結ぶと正n角形が得られる。とくにn＝17のとき、正十七角形を作図するということは、1の17乗根を作図するということであり、19歳の青年ガウスは、x¹⁷＝1の解法によってその作図方法を発見した。これがガウスをして数学の研究に向かわしめた発端であったといわれている。

［寺田文行］

[参照項目] | 円周等分多項式 | 複素数

ガウス平面〔図A〕

ガウス平面〔図B〕

ガウス平面〔図C〕

ガウス平面〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ガウス平面
ガウスへいめん
Gaussian plane

複素数平面あるいは単に数平面，z 平面ともいう。複素数の図表示に用いられる座標平面をいう。複素数 z＝x＋iy ( x ，y は実数) と直交座標平面上の点( x ，y ) とを一対一対応させて，このような平面上の点( x ，y ) が複素数 z を表わすものと考えたとき，この平面をガウス平面といい，この点( x ，y ) を複素数点という。複素数のこのような幾何学的表示法は，ノルウェーの C.ウェッセル (1745～1818) ，スイスの A.アルガン (1768～1822) がほとんど同時期に発見したが，今日のような形で論じたのは C.F.ガウスである。それでこの平面にガウスの名がついた。ガウス・アルガン平面，ガウス・ウェッセル平面という用語も使われる。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

ガウス平面 (ガウスへいめん)

→複素平面

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のガウス平面の言及

【複素平面】より

…直交座標を定めたxy平面において，点(a,b)が複素数α＝a＋bi(a,bは実数で，iは虚数単位)を表していると考えるとき，この平面のことを複素平面，またはガウス平面といい，点(a,b)のことを単に点αという。図1の点A,Bはそれぞれ複素数4＋4i，－5＋6iを表している。…

※「ガウス平面」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」