単位行列（読み）タンイギョウレツ（その他表記）unit matrix

デジタル大辞泉

たんい‐ぎょうれつ〔タンヰギヤウレツ〕【単位行列】

数学で、正方行列の対角成分が1で、それ以外が零である行列。同じ型の行列の積における単位元となる。すなわち単位行列をEとすると、行列Aについて、AE＝EA＝Aを満たす。

出典　小学館

ブリタニカ国際大百科事典 小項目事典

単位行列
たんいぎょうれつ
unit matrix

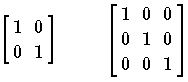n 次の正方行列 A＝(a_ij) において，主対角線上の要素がすべて 1で，その他はすべて 0であるものを n 次の単位行列という。たとえば，は，2次および 3次の単位行列である。任意の n 次の行列 A に対して，n 次の単位行列を E とすれば AE＝EA＝A なる関係が成り立つ。行列は，線形写像を表現するものと考えれば，恒等写像に対応する。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の単位行列の言及

【行列】より

…例えば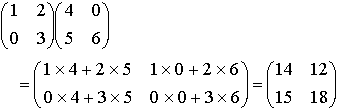，(m,n)行列Aと(n,k)行列Bとの積ABは(m,k)行列になる。n次正方行列についてのこの乗法において，群の乗法のときの単位元と同様の性質をもつのは各(i,i)成分が1で，他の成分がすべて0のもので，これをn次の単位行列という。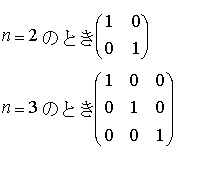(3)行列のスカラー倍　行列に対して，数や関数をスカラーという。…

※「単位行列」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」