可測関数（読み）かそくかんすう（その他表記）measurable function

改訂新版　世界大百科事典

可測関数 (かそくかんすう)
measurable function

空間Rのなかで，測度が定義される集合を可測集合といい，可測集合E（＝Rでもよい）の上で定義された関数fに対して，f（x）＞cとなる点xの全体をE_cとするとき，いかなる実数cに対してもE_cが可測集合であるような関数fを可測関数という。可測関数のf，gの一次結合や積は可測関数であり，任意のα≧0に対して｜f｜^αも可測関数である。またg（x）＝0なる点xを定義域から除けば，f/g，｜g｜⁻^α（α＞0）も可測関数である。可測関数の列｛f_n｝があって各点xで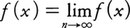が存在すればfは可測である。とくにユークリッド空間においてルベーグ可測集合を考える場合には，連続関数は可測関数である。負でない値をとる可測関数に対しては積分が定義せられ，任意の可測関数については，その正の部分，負の部分の少なくとも一方の積分が有限ならば，もとの関数の積分が定義される。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

可測関数
かそくかんすう
measurable function

可測集合 Aの上で定義された実数値をとる関数 fが与えられているとする。この値は有限でも無限でもよいと考える。この関数 fに対して任意の実数 aをとるとき，f≧aを満足する Aの点の集合，f＜aを満足する Aの点の集合，f＞aを満足する Aの点の集合，f≦aを満足する Aの点の集合のうちどれかが可測集合になるならば，fは Aの上で可測であるといい，fを A上の可測関数という。 f，gが有限の値をとる可測関数ならば，両者の和，差，積，最大値，最小値，商 (ただし f/gで g≠0) も常に可測である。

出典　ブリタニカ国際大百科事典 小項目事典