改訂新版 世界大百科事典 「同相」の意味・わかりやすい解説
同相 (どうそう)
homeomorphic
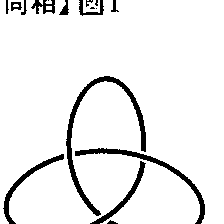
図形Aの点を図形A′の点にうつす対応が1対1対応で,この対応および逆の対応が連続であるとき,この対応をAからA′の上への同相写像,または位相写像といい,このような対応が存在するときAとA′は同相,または位相同型であるという。つまり,Aの各点PにはA′のちょうど1点P′が対応していて,(1)A′のどんな点P′をとってもP′に対応するAの点Pがちょうど一つ定まり,(2)Aの点QをPに近づくように動かせば対応するA′の点Q′はP′に近づき,逆にA′の点Q′をP′に近づくように動かせば対応するAの点QはPに近づくという性質をもつとき,AとA′は同相であるというのである。図形が薄いゴム膜でできているか,または薄いゴム膜の上に書かれているとき,それを裂いたり異なった点をくっつけたりせずにいろいろに延ばしたりねじったりすれば,初めの図形は変形するが,変形後の図形は元の図形と同相である。また,変形の途中で切り裂いても変形後に切れめの端を正確に前と同じにはり合わせれば,操作後の図形は元の図形と同相である。このようなわけで,例えば,円周は三角形の周,楕円の周や図1の結び糸の形の曲線に同相である。同相な図形に共通な性質を位相的性質といい,この性質を主たる研究対象とする幾何学を位相幾何学という。
→位相幾何学
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報