位相幾何学（読み）イソウキカガク（その他表記）topology

デジタル大辞泉

いそう‐きかがく〔ヰサウ‐〕【位相幾何学】

図形の性質の中で、寸法や曲直とは無関係に、位置関係などの位相的性質を対象とする幾何学。オイラーおよびポアンカレによって初めて組織的に研究された。狭義の位相数学。トポロジー。

出典　小学館

精選版 日本国語大辞典

いそう‐きかがくヰサウ‥【位相幾何学】

1. 〘 名詞 〙 位相写像によって不変な、幾何学的図形の性質や、連続写像自身の性質を研究する、連続の幾何学。狭義の位相数学。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

位相幾何学 (いそうきかがく)
topology

トポロジーともいう。図形を構成する点の連続的位置関係のみに着目する幾何学。

同相と同位

点相互の連続的位置関係を変えることなく，互いに変形して重ね合わすことができる二つの図形は同じ図形とみなされ，互いに同相であるという。図形がゴムで作られていると考えよう。図形は伸び縮みの変形ができるが，この図形を切り裂いたり重ね合わせたりせずに，伸び縮みだけで変形した図形は元の図形に同相である。さらに，図形の一部分を切り離して，伸縮変形をした後に，再び切り離した部分をもとどおりにはり合わせても，図形上の点相互の連続的位置関係が保たれるので，同相な図形が得られる。文字Sは引き伸ばすと文字Iに変形するので，SとIは同相である。しかし，Iはどのように伸び縮みさせても，両端を重ね合わさぬかぎり，文字Oには変形しないので，IとOは同相でない。アルファベット文字のいくつかを位相幾何学的に分類すると下記のようになる。同じ列の文字は互いに同相であり，異なる列の文字は互いに同相でない。

　CILMNSUVWZ

　EFTY

　DO

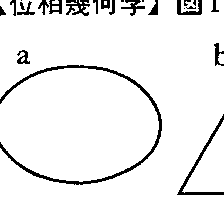
図1でa～cとd～gの図形は互いに同相である。図1-aは円，図1-bは三角形，図1-cは空間で結んだ円である。図1-dはドーナツの表面で数学ではトーラスtorusと呼ばれる曲面である。図1-eは結んだトーラス，図1-fは球にひと結びしたトンネルを掘った立体の表面である。図1-gはコーヒーカップの表面である。図1-aと図1-bは伸び縮みで互いに変形することができるが，図1-cは伸び縮みだけでは図1-aに変形できない。図1-aは，l点Pで切り離してひと結びし，再び切り離した点Pをつなぐと図1-cに変形できる（図2-a）。コーヒーカップの表面はトーラスに変形できるが，図1-e，図1-fは切り離し変形なしにはトーラスに変形できない。図1-eは，図上の小円Cで切り離して結び目をほどき，再びCをはり合わせると図1-dになる（図2-b）。図1-fについては，トンネルの入口の円Cで曲面を切り離し，切り離されたトンネルの表面を球の内部で結び目をほどきながら他方の出口から引き出し，引き出された部分を球の外で伸ばして再びCをはり合わせると図1-dに変形できる（図2-c）。

　このように，位相幾何学は図形それ自身の連続的形状を問題にするが，また平面や空間に対する図形の位置関係も重要な研究対象とする。平面上の円は平面を二分する。この性質は，円と同相である平面上のどんな図形についても成立している。〈平面上における円と同相な図形は，平面を二つの領域に分ける（ジョルダンの曲線定理Jordan's curve theorem）〉は平面位相幾何学における基本定理である。空間における円と同相な図形は空間を二分しない。ジョルダンの曲線定理は，円とそれを含む平面との位置関係を示す定理である。平面上で，伸び縮み変形のみで互いに重ね合わすことができる図形は，その平面上で同位な図形と呼ぶ。空間においても，伸び縮みのみの変形で互いに移動できる図形は，空間内で同位な図形と呼ぶ。切りはりによる変形は，図形上の点相互の連続的位置関係を変えないが，空間に対する図形の位置関係を不連続的に変える。同位である図形は，互いに同相である。図1-aと図1-bは同位であるが，図1-aと図1-cは同位でない。図1-cは切りはりをしないと図1-aに変形できないからである。同じ理由で図1-e，図1-fは図1-dに同位でない。コーヒーカップの表面はドーナツの表面に同位である。空間における円と同相な図形は結び目（結び）と呼ばれ，結び目の同位問題は現代数学の対象として研究されている。以上のように，位相幾何学は図形の位置と形相に関する直観に本質的に訴える幾何学といえるが，このことが位と相の幾何学，すなわち位相幾何学の名の由来である。

トポロジー

位相幾何学はトポロジーとも呼ばれるが，これはギリシア語のtopos（場所）とlogia（学）に由来し，リスティングJ.B.Listing（1808-82）の著書《トポロジーへの試論Vorstudien zur Topologie》（1847）にはじまる。リスティングはトポロジーを〈空間の中の点，線，面および位置について，量や大きさとは別の，形状，位置を示す法則を研究する学問〉と定義している。さらに古く，G.W.F.ライプニッツは1679年C.ホイヘンスにあてた手紙の中で〈代数学が量を扱うのに対し，直接に幾何学的な位置を扱う解析学の一つの分野が必要であると思う〉と述べ，この分野を位置解析学analysis situsと名付けたが，何一つ具体的問題にはふれていない。analysis situsという言葉は，20世紀初期まで長く通用していたが，今日この言葉は用いられない。

位相不変量－－オイラー標数

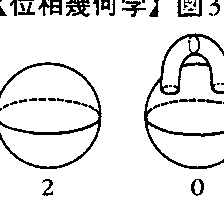
正多面体は5種類あり，すべて互いに同相である。どの正多面体についても，その頂点の数をa，辺の数をb，面の数をcとすると，a－b＋c＝2が成り立つ。このことは正多面体にかぎらず，球面に同相であるどんな多面体についても成立している。多面体の研究の歴史はギリシアにさかのぼるが，この事実は，1640年になって初めてR.デカルトにより発見され，1752年L.オイラーにより再発見されている。一般に多面体の頂点の数aと面の数cとの和から辺の数bを引いた数a－b＋cをその多面体のオイラー標数Euler's characteristicという。同相な多面体のオイラー標数は等しい。このように同相な図形に共通な性質は，図形の位相的性質といわれ，オイラー標数のような量は位相不変量という。物体の表面は曲面である。無限に広がる平面も曲面であり，円板のように縁のある曲面もあるが，物体の表面は無限に広がらず，縁もない。このような曲面を閉曲面という。閉曲面は多面体と同相であることが知られている。したがって閉曲面のオイラー標数が，その曲面と同相な多面体のオイラー標数として定義される。物体の表面である閉曲面の位相的性質は，そのオイラー標数で決定される。物体の表面である閉曲面がとりうるオイラー標数は2，0，－2，－4，……，－2n，……（nは自然数）であり，与えられたオイラー標数をもつ閉曲面は容易に作れる。球にg個の取っ手をつけた立体の表面である閉曲面のオイラー標数が2（1－g）になる（図3-a）。g個の穴のあいたビスケットの表面といってもよい（図3-b）。gを閉曲面の種数genusと呼ぶ。（曲面の種数）＝1－1/2（オイラー標数）であり，したがって種数も曲面の位相不変量である。物体の形は数限りなく多様であるが，どんな物体の表面も，いくつかの穴のあいたビスケットの表面と同相になるのである。曲面は物体の表面にかぎらず，円板のように縁のある曲面もある。閉曲面からその上にあるいくつかの円板の内部を取りのぞくと縁のある曲面が作れるが，このような曲面と位相的性質を異にする縁のある曲面が，1858年にメービウスにより発見された。この曲面はテープを180度ひねって両端をはり合わせて作られる曲面でメービウスの帯Möbius' stripと呼ばれる（図4-a）。メービウスの帯の縁は円と同相である。この曲面の中心線c上の1点pを出発して，中心線cに沿って一周すると裏側にでてくる。このように，曲面の内部の1点から出発して，縁と交わらずに裏側に回ることができる曲面を単側曲面と呼ぶ。単側曲面は，いわば表と裏のない曲面であり，その縁を境目として表裏の色分けが不可能な曲面である。これに対し，円板のように，表と裏を縁を境目として色分けできる曲面，あるいは縁を通らずに表から裏へでられぬ曲面を両側曲面と呼ぶ。単側性は位相的性質である。メービウスの帯の中心線上の1点pに小さい円を書き，円上に左回りに矢印をつけておく。この小円を中心線に沿って一周させて元の点pに帰ってくると，矢印は右回りについている（図4-b）。このことからメービウスの帯は向き付け不能な曲面と呼ばれる。数学では曲面は〈各点の近傍が円板と同相である図形〉と定義されるが，曲面の位相的性質は，その曲面の境界の数，オイラー標数，向き付けの可能性の3条件で決定される。

一筆書きの問題

頂点と呼ばれる有限個の点と，それらを結ぶいくつかの線からなる図形を線状グラフという。線は頂点以外で互いに交わらないものとする。鉄道網，回路網，結晶構造図，系統図など線状グラフの例は多い。線状グラフの位相幾何学の一例として，一筆書きの問題がある。線状グラフの1点から出発して，どの線もただ1回だけ通過して，元の点に帰ることができる場合に，その線状グラフは一筆書きができるという（頂点は何回通過してもよい）。線状グラフが一筆書き可能か否かは線状グラフの位相的性質である。ある頂点に集まる線の数をその頂点の次数と呼び，その次数が奇数である頂点を奇点，偶数である頂点を偶点と呼ぶ。このとき次の一筆書きの基本定理が成り立つ。〈ある線状グラフが一筆書きできるための必要十分条件は，線状グラフが連結であり，奇点の数が0か2である〉。一筆書きの問題はオイラーにはじまる。オイラーは1763年次の問題を提出し，その冒頭に〈次のようなのが，おそらくライプニッツのanalysis situsの問題であろう〉と述べている。オイラーの問題〈ケーニヒスベルクにはクナイプホーフという島Aがある。この島によって川は図5-aのように，二つの支流に分かれている。7個の橋a，b，c，d，e，f，gがこの支流に架けられている。これらの橋の全部を1回だけしか渡らないように歩くことができるか〉。この問題は，橋を線とし，川で分けられた四つの陸地を点とみなして，線状グラフ（図5-b）の一筆書きの問題になる。このグラフでは，いずれの頂点も奇点で，奇点の数が5であり，一筆書きができない。

ホモトープとホモローグ

ライプニッツに予見され，オイラーら二，三の数学者がいくつかの仕事をしたにすぎない位相幾何学は，19世紀に入るとC.F.ガウス，G.F.B.リーマンらの研究を通じてしだいにその重要性が認められてくる。とくにリーマンは当時数学の最高峰の一つと考えられていた代数関数の積分－－アーベル積分の理論において，曲面の種数の概念が基本的に重要であることを示している。さらに19世紀後半になると，J.W.R.デデキント，M.B.カントールにより実数の概念が確立するとともに，カントールによる点集合論の研究がはじまる。このような状況の下で，位相幾何学が学として独立の分野を確立するのは，H.ポアンカレによってである。1895年にはじまるポアンカレの位相幾何学に関する一連の研究は，ホモトープhomotopicとホモローグhomologusという二つの概念を基礎にしている。点が動くと曲線になる。出発点を始点と呼び，到着点を終点と呼ぶ。曲線は途中で交わっていてもよい。始点と終点が一致する曲線を閉曲線closed curveという。二つの閉曲線は互いに連続的に変形しうるときに，互いにホモトープであるという。変形の途中で曲線が自分自身と交わってもよい。これが同位との相違である。また閉曲線が1点に縮むとき，ホモトープ0の閉曲線という。ある図形上の二つの閉曲線が，その図形上で互いに連続的に変形しうるとき，これらの閉曲線はその図形上で互いにホモトープという。またある図形上の閉曲線が，その図形上で1点に縮むとき，その図形上でホモトープ0であるという。図6-aでトーラス上の二つの閉曲線aとbはトーラス上で互いにホモトープであり，cはトーラス上でホモトープ0である。閉曲線dは重複点のある閉曲線であるが，aとホモトープである。図6-bのように，くびれた部分がだんだん小さくなり消滅してaに変形する。aとbは同位であるが，aとdは同位でない。球面上にどんな閉曲線を書いても，その閉曲線は球面上でホモトープ0である。ところがトーラス上の閉曲線a（図6-a）はホモトープ0でない。図形上にホモトープ0にならない閉曲線が存在するか否かは，その図形の位相的な性質である。このことから球面とトーラスが同相でないことがわかる。ホモトープ0である閉曲線は1点に縮まるので円板をはることができる（図7-a）。閉曲線は自分自身と交わっていることもあるので，円板も自分自身と交わっていてもよい（図7-b）。一般に閉曲線が曲面の境界であるとき，ホモローグ0の曲線という。二つの閉曲線が一つの曲面の境界になるとき，この二つの閉曲線は互いにホモローグであるという。ある図形上にある二つの閉曲線が，その図形上にある曲面のちょうど境界になっているとき，これらの閉曲線は，その図形の上で互いにホモローグであるという。互いにホモトープな閉曲線は，互いにホモローグであり，ホモトープ0である閉曲線はホモローグ0である。種数2の閉曲面（図8）上の閉曲線cは，cで分けられる曲面Fの境界であるから，この曲面上でホモローグ0であるが，1点に縮まないのでホモトープ0でない。ある図形上で互いにホモローグでない閉曲線がn個あり，どんな閉曲線もこれらn個の閉曲線のいくつかの和集合とホモローグになるとき，この図形の一次元ベッチ数Betti numberがnであるという。ベッチ数は図形の位相不変量である。種数gの閉曲面の一次元ベッチ数は2gになる。したがって閉曲面の位相的性質は一次元ベッチ数で決定されるといえる。閉曲面において（オイラー標数）＝2－（一次元ベッチ数）である。オイラー標数が位相不変量であることが，この式からわかるが，この式をオイラー=ポアンカレの公式という。

位相幾何学の現状

20世紀の数学は，その位相性と代数性を基礎として，公理的に構成されている。連続性が議論できる空間は位相空間といい，図形も一種の位相空間である。位相を定める基本的諸概念は近傍，開集合，閉包などである。これらの概念を基礎に集合論的手法で位相空間およびその部分集合の位相的性質を研究する分野を集合論的位相幾何学あるいは一般位相幾何学general topologyという。この分野はカントールによる点集合論の流れをくむ分野であり，次元の問題はこの分野に属している。位相不変量として次元の概念を設定する問題と方法は，今世紀のはじめにポアンカレにより提示されたが，L.E.ブローエルらによる数学的定式化を経て，今日ほぼ完成の域に達している。ホモトープ，ホモローグの概念は，今世紀前半を通じて位相的，代数的に整備され，代数的位相幾何学として一分野を形成している。代数的位相幾何学は，位相空間に代数的構造を対応させ，空間の位相的構造を代数的構造で表現する。図形上の閉曲線の全体はホモトープの概念で分類することにより群となるが，この群を基本群と呼ぶ。またホモローグの概念で分類した閉曲線全体も群となり，一次元ホモロジー群と呼ばれる。球面の一次元ホモロジー群は単位元のみからなる群であるが，トーラスの一次元ホモロジー群は，整数全体の作る加法群Zの二つの直和Z＋Zに同形になる。これらの群構造の相違が，球面とトーラスの位相構造の相違を表現している。基本群，一次元ホモロジー群は高次のホモトピー群，ホモロジー群に拡張されるが，さらに20世紀後半には，空間に対応させる代数的構造はますます多様化し精密化され，代数的位相幾何学は位相幾何学における基本的分野と考えられている。

多様体

高次元の概念は19世紀中ごろすでに確立されていたが，高次元曲面の概念はリーマンによる。リーマンによる高次元曲面は20世紀前半において多様体manifoldとして定式化され，多様体は数学における一つの基本的図形とみなされ，その位相幾何学的研究は位相幾何学の一つの中心となっている。高次元多様体の位相構造はホモトピー論を通して代数的位相幾何学の研究に帰着する場合が多いが，三次元および四次元多様体の位相構造の研究は固有の困難さを伴っている。〈基本群が単位元のみからなる三次元閉多様体は三次元球面と同相か〉という問題はポアンカレにより提出され，ポアンカレの予想Poincaré conjectureといわれるが，完全な解決に至っていない。微分多様体は，その各点の近傍で微分という操作が可能な多様体であり，直観的には滑らかな多様体である。したがって微分多様体上では解析学が可能である。微分多様体上の解析学は，位相幾何学と解析学の重要な接点であり，微分多様体上の微分構造の研究，微分多様体間の微分可能写像の研究など重要課題が多い。〈七次元球面上には本質的に相異なる微分構造が存在する〉ということをミルナーJ.W.Milnorが1956年に発見して以来この分野は急速に発展したが，ミルナーによりこの分野は微分位相幾何学と名付けられている。力学系の位相幾何学的研究，トムR.Thomによるカタストロフィーの理論などはこの分野に属している。

単体と複体

ポアンカレはホモロジー概念を厳密に導入するため，図形を単純な図形－－単体の集合体，すなわち複体として構成した。0次元の単体は点であり，一次元単体は線分，二次元単体は三角形（内部も含む），三次元単体は四面体である（図9）。一般にn次元単体はn次元ユークリッド空間の（n＋1）個の独立な点を含む最小凸体である。いくつかの単体をその境界である辺単体ではり合わせて構成される図形が多面体である。複体は単体とそのはり合わせ方をあわせ考えた数学的構造であり，多面体上の一つの構造と考えられる。この構造を用いて多面体の位相的性質を研究する分野は組合せ位相幾何学，あるいはPLトポロジーpiecewise linear topologyと呼ばれている。複体的構造が同形である多面体は同相である。逆に〈同相な多面体は，その複体的構造を適当に細分すると同形な複体的構造になるか〉という問題は組合せ位相幾何学の基本予想といわれていたが，61年ミルナーにより否定的に解決された。〈多様体は多面体に同相になるか〉という問題は多様体の三角形分割問題と呼ばれ，微分多様体についてはケアンズS.S.Cairnsにより1935年に肯定的に解決されたが，位相多様体には多面体に同相にならないものが存在することが知られている。

不動点定理

位相幾何学では図形の位相構造の研究とともに，図形間の連続写像の研究も重要課題である。円板から円板自身への連続写像をfとすると，f（P）＝Pなる点，すなわち不動点が存在する。この定理はブローエルの不動点定理と呼ばれている。不動点定理は多様に一般化されて，広い応用範囲をもっている。微分方程式の解の存在定理をはじめ，一見連続性とほど遠いと考えられる整数論における解の存在性の問題についても適用されるのみならず，経済学における均衡状態の存在性の問題などその適用範囲は広い。

　位相幾何学には四色問題のように比較的孤立した問題もあるが，全体として有機的に一つの研究体系を形成しており，20世紀数学の一つの基盤として，すべての数学の分野に深く浸透している。
執筆者：田尾 鶉三

図1～図2

図3～図9

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

位相幾何学【いそうきかがく】

トポロジーとも。幾何学的図形（空間）の位相的性質を研究する幾何学の部門。空間AからBへの写像が一対一，連続で，BからAへの逆写像も連続なとき，この写像を位相写像，AとBを同位相であるといい，位相写像で不変な性質，つまり同位相の空間に共通する性質を位相的性質という。位相幾何学の古典的問題としては，多面体のオイラーの定理，ケーニヒスベルクの橋の問題，地図の四色(ししょく)問題などがある。→位相空間／位相数学／数学
→関連項目幾何学｜曲面｜三体問題｜トポロジー｜一筆書き｜結び目理論｜メービウスの帯

出典　株式会社平凡社

日本大百科全書(ニッポニカ)

位相幾何学
いそうきかがく

→トポロジー

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

位相幾何学
いそうきかがく

「トポロジー」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の位相幾何学の言及

【位相】より

…(1)数学用語。トポロジーtopologyともいう。数学において極限や連続の概念は中心的役割を演ずるが，これらの概念は実数の集合や平面上の点集合については“近さ”とか“近づく”といった概念を用いて定義される。…

【幾何学】より

…そこで，同相写像によって変わらないような性質を研究する幾何学というものが考えられる。トポロジーtopologyはこのような研究を主目的とする数学であって，位相幾何学と訳されているように，この幾何学では図形の位置や形相に関した性質で，点の連続性にのみ依存する性質が扱われる。位相幾何学は位置解析学analysis situsという名称でG.W.ライプニッツによって予見されていたが，具体的な業績はオイラーによって初めて与えられた。…

【トポロジー】より

…集合上に〈近さ〉とか〈近づく〉といった概念で表される構造が与えられると，その集合上で極限や連続について論ずることができるが，このような構造をトポロジー(訳して位相)と呼ぶ。また，この構造が内容や方法上で問題となる数学のことを広くトポロジー(訳して位相数学)と呼ぶこともあるが，ふつうはもっと狭く，図形の位置や形状に関する性質で，図形を構成する点の連続性にのみ依存するものを研究の対象とする数学のことをトポロジー(訳して位相幾何学)と呼ぶ。…

【幾何学】より

…なお，リーマン空間では長さを不変にする変換は一般に恒等変換しかないから，リーマン幾何学はクラインの意味での幾何学とはいえず，リーマン幾何学の発展はエルランゲン･プログラムの思想に破綻（はたん）を生ぜしめた。
［位相幾何学］
　先に，ユークリッド幾何学，射影幾何学では，それぞれ合同変換，射影変換によって変わらないような幾何学的性質が研究されると述べたが，合同変換や射影変換よりはるかに一般的なものに位相変換または同相写像と呼ばれるものがある。これは二つの図形の間の1対1対応で，それおよびその逆写像が連続となるようなものである。…

【トポロジー】より

…集合上に〈近さ〉とか〈近づく〉といった概念で表される構造が与えられると，その集合上で極限や連続について論ずることができるが，このような構造をトポロジー(訳して位相)と呼ぶ。また，この構造が内容や方法上で問題となる数学のことを広くトポロジー(訳して位相数学)と呼ぶこともあるが，ふつうはもっと狭く，図形の位置や形状に関する性質で，図形を構成する点の連続性にのみ依存するものを研究の対象とする数学のことをトポロジー(訳して位相幾何学)と呼ぶ。リスティングJ.B.Listingは1847年に著書《Vorstudien zur Topologie》を出版し，トポロジーということばを使っているが，この数学の実質的創始者であるH.ポアンカレは，この数学をanalysis situs(位置解析学)と呼び，長らくこのことばが使われていた。…

※「位相幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」