対角線論法（読み）たいかくせんろんぽう（英語表記）diagonal method

改訂新版　世界大百科事典

対角線論法 (たいかくせんろんぽう)
diagonal method

証明の論法の一種であり，考察している対象を縦横が無限の長さをもつ表に並べてその対角線上に並んだものを利用して議論する方法である。G.カントルによって集合で初めて使われた。〈0＜x＜1である実数全体の集合Iは非可算である〉ことを示す彼の論法を見てみよう。0＜x＜1である実数は小数0.a₁a₂a₃……と表せる。xが有理数のときは有限小数で表せるが，例えば0.32000……のように後に0が続いていると考える。さて，I＝｛x｜0＜x＜1｝は可算集合であると仮定しよう。するとIのすべての元は，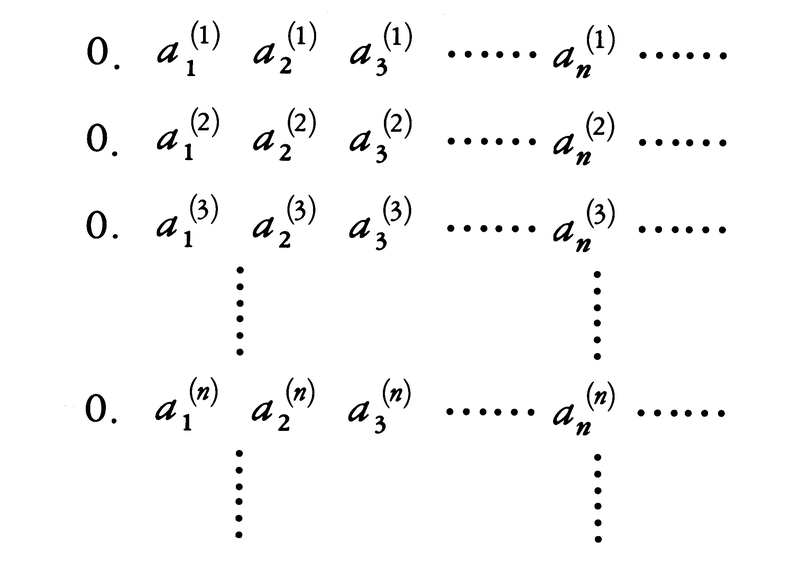

と並べることができる。そこでこの表の対角線に出てくる数字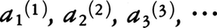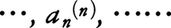を取り出し，小数β＝0.b₁b₂b₃……b_n……をa_i⁽ⁱ⁾≦4であればb_i＝6，a_i⁽ⁱ⁾≧5であればb_i＝1と定義する。もちろん0＜β＜1であるが，作り方よりβは上の表には現れない。一方，上の表は0＜x＜1である実数をすべて含んでいるので，これは矛盾である。したがってIは非可算集合である。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」