日本大百科全書(ニッポニカ)「有理数」の解説
有理数
ゆうりすう
整数と分数をあわせた数のすべてを有理数という。有理数は、整数の商で表される数、すなわち、mを0でない整数、nを整数としてn/mの形に書かれる数である。
有理数には、正・負の整数、分数と0が含まれる。
一つの有理数はいろいろな形に表すことができる。n/m,n′/m′（m、n、m′、n′は整数、m、m′は0でない）が同じ有理数を表すのは、nm′=n′mのときである。
二つの有理数の和・差・積は有理数であり、有理数を0でない有理数で割った商も有理数である。しかし、正の有理数の平方根は、有理数とは限らない（例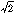 
）。有理数でない実数が無理数である。これらの関係は次のようになる。
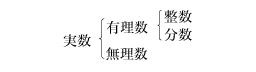
有理数は、小数で表すことができる。その場合、有限で終わる小数（有限小数、例 3/4=0.75）か、小数部分のある位以下で同じ数字が限りなく繰り返されるような小数（循環小数、例 5/11=0.454545……）のどちらかになる。また循環小数は有理数を表す。
有理数は、大小の順序に従って直線上に並べることができる。これが数直線である。数直線上で、二つの有理数をとると、その間には、少なくとも一つの（したがって無数の）有理数がある。これを有理数の稠密(ちゅうみつ)性という。
［三輪辰郎］
[参照項目] | |
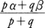はαとβの間の有理数であるから，αとβの間には有理数が無限に存在する。