小数（読み）ショウスウ

デジタル大辞泉

しょう‐すう〔セウ‐〕【小数】

１ 1より小さい正の実数。
２ 整数でない実数を、小数点を用いて十進法で表した数。0.1のように整数部分を含まないものを純小数、1.23のように整数部分を含むものを帯小数という。

出典　小学館

精選版 日本国語大辞典

しょう‐すうセウ‥【小数】

1. 〘 名詞 〙
2. ① 小さな数。少数。
   1. [初出の実例]「実に無用有害の小虫と申ながら彼も億万生霊の小数(セウスウ)なり」(出典：安愚楽鍋（1871‐72）〈仮名垣魯文〉三)
3. ② 一よりも小さい正の実数。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
4. ③ 整数でない実数を十進法で表わしたもの。〔改正増補和英語林集成（1886）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

小数
しょうすう

1の10分の1を0.1、その10分の1を0.01、さらにその10分の1を0.001、……のように表し、それらを単位と考えて、1より小さい数を、たとえば、
　　0.1×4＋0.01×3＋0.001×5
を0.435のように表したとき、これを小数という。このとき、0と4の間に書いた点を小数点という。また、小数0.435で、4は小数第1位の数字、3、5はそれぞれ小数第2位、第3位の数字である。整数と小数の和、たとえば、2＋0.435は2.435のように書く。このような数を帯小数という。

　小数は、十進位取り記数法(じっしんくらいどりきすうほう)を1より小さいほうへ広げたものといえる。そこで、小数の四則計算は、整数の四則計算と同じように考えてできる。加法は、0.435＋0.321＝0.756のように、小数の各位ごとに足せばよい。ただし、0.06＋0.05＝0.11のように、同じ位の数の和が10を超すときは、上の位に繰り上がりがある。減法も同じようにする。乗法、たとえば、0.43×0.026では、まず、小数点を考えないで43×26＝1118を計算し、次に、乗数、被乗数の小数点より下にある数字の数の和5を求め、積の小数点より下の数字の数がそれと一致するように、小数点を打つ。この場合は、0.43×0.026＝0.01118となる。除法、たとえば、0.2451÷0.43では、除数0.43を100倍して整数にするとともに、被乗数も100倍して24.51とし、24.51÷43を計算すればよい。この計算では小数点を含まない2451÷43を計算して57を求め、小数点を、被除数24.51から0.57のように決める。つまり、0.2451÷0.43＝0.57である。また、0.2477÷0.43では、同じように、2477÷43から商57、余り26を得るが、商の小数点は、前と同じようにして0.57、余りのほうは、初めの被除数0.2477から、0.0026となる。

　小数は分数に表すことができる。0.1＝1/10、0.01＝1/100、……で、0.435＝435/1000となる。逆に、分数は小数に表すことができる。分数を既約分数に直したとき、分母が2、5の累乗の積であれば、7/80＝7/(2⁴×5)＝0.0875のように、有限で終わる小数（有限小数）になるが、分母が2、5以外の因数を含んでいると、限りなく続く小数（無限小数）になる。たとえば1/7では0.142857142857……と、142857を無限に繰り返す。これを0.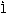4285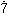のように、繰り返す部分（循環節という）を点で挟んで表す。また、19/55＝0.34545……＝0.3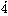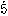となる。このように、どこまでも同じ数字を繰り返す小数を循環小数という。分数を小数に表すと、有限小数か循環小数のどちらかになる。無理数も小数に表すことができるが、そのときは、循環しない無限小数になる。

　これまで述べてきた小数は、1の10分の1を0.1のように表したもので、十進小数という。これに対して、1の2分の1を0.1のように表した二進小数が考えられる。古代バビロニアでは、六十進小数が考えられていたといわれる。

［三輪辰郎］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

小数
しょうすう
decimal

ある数 a は0と1の間にある ( 0＜a＜1 ) はんぱな数であるとすると，数 a は，数字 p，q，r，s，… を用いて
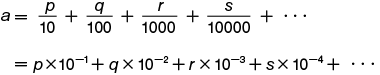と表わすことができる。これを整数の十進法と類似の方法で，a＝0.pqrs… と書き，小数と呼ぶ。0と p の間の点を小数点といい，たとえば正の整数 28と小数 0.735との和は，28＋0.735＝28.735 と書く。この正の整数と小数の和を，帯小数あるいは単に小数と呼ぶ。小数点より左側の部分を整数部分，右側の部分を小数部分という。小数には 1/4＝0.25 のような有限小数，1/3＝0.3333… のような循環小数，√2＝1.41421356… ，また π＝3.14159265… のように循環しない無限小数がある。有限小数および循環小数は，m ，n を1でない整数とすれば，必ず m/n で表わされる (有理数である) が，無限小数は m/n の形で表わすことはできない (無理数である) 。東洋では古くから分数よりも小数がよく使われたが，西ヨーロッパではオランダの数学者 S.ステビーン (1548～1620) が初めて使用したといわれる。彼の表記法は現在のものと異なり，たとえば 28.735を，28◯7◯3◯5◯ (丸の中にはそれぞれ位を意味する1，2，3，4が入る) のように小数点を使わずに表わした。小数の考案により1より小さい (正の) 数も，整数と統一的に十進法で表記することが可能となり，数直線に目盛られたものとしての，近代的な実数概念が始った。また，無限小数は近代的な極限概念の萌芽ともいわれる。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

小数 (しょうすう)
decimal

実数を表示する一つの方法である。1.75，1/7＝0.142857142857……のように，有限または無限に続く数字の列のあるところに点をつけたものを小数といい，点 ・ のことを小数点という。小数点の次の位置を小数第1位，その次を小数第2位などという。1.75は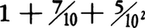を表すが，このように有限で終わるものを有限小数という。1/7＝0.142857142857……のように無限に続くものを無限小数という。無限小数のうち，上の例1/7の142857のように，あるところ以後は同じ数字の配列が繰り返されるものを循環小数という。整数は2＝2.0のように小数で表示される。また有理数は有限小数か循環小数で，無理数は循環しない無限小数で表される。

　小数325.67832を3.2567832×10²と表示する方法がある。前者を固定小数点表示，後者を浮動小数点表示という。

　上に述べたのは，十進法の小数であるが，他の進法においても小数の表示が用いられる。例えば二進法で1.01は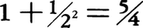を表す。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

小数【しょうすう】

実数を，小数点を用いて十進法で書き表したもの。小数点以下第１位，第２位，…の数字は1/10，1/100，…の位を表す。小数点以上の数が０でないときは帯小数といい，小数点以上を整数部分，以下を小数部分という。帯小数でない小数を純小数ということもある。小数部分が有限個の桁(けた)で終わるものを有限小数，そうでないものを無限小数という。→循環小数
→関連項目帯小数

出典　株式会社平凡社

普及版 字通

【小数】しようすう

小術。

字通「小」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の小数の言及

【記数法】より

…ギリシアのイオニア式記数法も同様な長所をもっている。　1より小さい数を表すのにわれわれは十進小数を使っている。小数そのものは，メソポタミア，中国で古くから使われていたが，オランダのステフィン(ステビンともいう)Simon Stevin(1548‐1620)は統一的に十進小数を使うべきことを主張し，それを広めた。…

※「小数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」