帰納的関数（読み）きのうてきかんすう

改訂新版　世界大百科事典

帰納的関数 (きのうてきかんすう)

〈実際effectiveに計算可能な関数〉に関する数学的概念であるリカーシブ関数recursive functionに対して，日本で定着している術語。1931年，K.ゲーデルが原始帰納的関数として初めて定式化し，これを用いて不完全性定理の証明を得た。自然数｛0，1，2，……｝の上で定義され，自然数を値とする関数f（x₁，……，x_n）が，

　f（x）＝x＋1　……（1）　

　f（x₁，……，x_n）＝q　（qは定数）　……（2）　

　f（x₁，……，x_n）＝x_i　（1≦i≦n）　……（3）　

　f（x₁，……，x_n）＝g（h₁（x₁，……，x_n），……，h_m（x₁，……，x_n））　……（4）　

　（ここで，gはm変数の関数で，g，h₁，……，h_mはすでに与えられた関数）

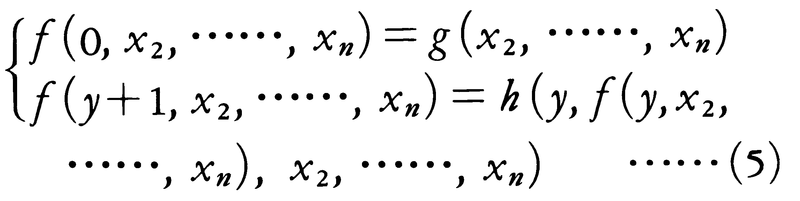
　（ここで，g，hはすでに与えられた関数で，n＝1のときg（　）は定数を表すものとする）

を有限回適用して定義されるとき，原始帰納的関数primitive recursive functionという。次に，μyR（＊，y）は，命題R（＊，y）が成り立つようなyが存在するときそのようなyの最小数を値とし，そうでないときは値が定まらないものと規約する。関数f（x₁，……，x_n）が上の（1）～（5）および，

　f（x₁，……，x_n）＝μy［g（x₁，……，x_n，y）＝0］　……（6）　

　（ここで，gはすでに与えられた関数で，すべての自然数の組x₁，……，x_nに対して，つねにg（x₁，……，x_n，y）＝0を満たすようなyが存在するものとする）

を有限回適用して得られるとき，一般帰納的関数general recursive functionという。このような定式化および帰納的関数の理論recursion theoryの発展にはクリーネS.C.Kleeneの寄与に大きく負うている。なお，一般帰納的関数はチューリング機械によって計算可能な関数と一致した概念である。
→計算可能性　→数学基礎論
執筆者：柘植 利之

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の帰納的関数の言及

【計算モデル】より

…　RAMより計算できる関数と，チューリング機械によって計算できる関数と，ラムダ計算で計算できる関数はすべて同じであることを示すことができる。また，これは帰納的関数として定義できる関数であることを証明することができる。これらのことから，コンピューターにおいて計算するアルゴリズムが存在するという直観的な概念を，これらの計算モデルで計算できることとして定義してよいことがわかる。…

※「帰納的関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」