数学基礎論（読み）すうがくきそろん（英語表記）foundations of mathematics

精選版 日本国語大辞典

すうがく‐きそろん【数学基礎論】

〘名〙 数学の基礎に関する理論。集合論で発生した逆理を解決するための努力の集積として二〇世紀初頭に成立した。数学の論理的構造を分析するための有力な手段として記号論理学を用いるので、後者の一分科と考えられることもある。なお、この理論の成果は数学だけでなく、応用数学、計算機の基礎理論などにも影響を及ぼしている。

出典　精選版 日本国語大辞典

デジタル大辞泉

すうがく‐きそろん【数学基礎論】

数学の基礎に関する理論。19世紀に導入された集合論が逆理（逆説）を派生させたが、その反省から生まれた、数学とはいかなるものであるべきかの理論。20世紀初頭に成立。記号論理学を用いる。

出典　小学館

改訂新版　世界大百科事典

数学基礎論 (すうがくきそろん)
foundations of mathematics

数学は矛盾のない理論体系と信じられており，諸科学の中でももっとも厳密な論証を誇るものとして，およそそのよって立つ基盤がゆらぐようなことがあろうなどとは考えられなかった。ところが，19世紀末G.カントルによって創設された集合論はまもなく逆理を生じた（パラドックス）。カントル自身が発見した逆理（1899），ブラリ=フォルティの逆理（1897）やラッセルの逆理（1903）がそれである。集合論におけるすこぶる有効な用法ときわめて類似したしかたによって容易にこれらの逆理が導かれるのみならず，同時期に提出されたリシャールの逆理（1905）〈25字以内の字数によっては定義されない最小の自然数は，現にこの文章によって25字で定義されている〉とともに，ほとんど形式論理の範囲内で現れることから数学は重大な危機に陥った。例えば，ラッセルの逆理は次のようにして生ずる。自分自身を要素として含まないような集合tの全体をTとしよう。すなわちT＝｛t｜t∉t｝。いま，T∈Tと仮定すると，Tの定義から，T∉Tとなり仮定に矛盾する。したがって，T∉Tであるが，このとき再びTの定義よりT∈Tとなり，これは二律背反である。

　集合論が世に現れてから数学上の概念構成は集合概念を用いることにより著しく円滑にかつ統一的になった。カントルの集合論はきわめて有力な数学理論であるのみならず，数学全般にわたる基礎的理論であることがしだいに認められるようになり，自然数論や実数論，ひいては解析学，代数学，幾何学など数学における各理論を集合論の中で展開することが原理的に可能であることがわかってきた。J.W.デデキントは，実際に，集合概念と1対1対応の概念とから自然数の体系を作れることを示し（1888），さかのぼって実数を有理数（有理数の体系は自然数の拡張として容易に構成できる）の集合A，Bの組（A，B）として定義し（1872），A.L.コーシーやK.ワイヤーシュトラスと並んで，それまで直観的にしか把握されていなかった実数の概念，ひいては解析学に厳密な基礎を与えた。集合論に現れた逆理は，H.ワイルによれば，〈数学の王国のごく辺境に生じた紛争にすぎず，王国の大部分はなお安寧であるとみられるかも知れない〉が事態は決してそのようなものではなく，数学における集合論の影響があまりにも大きいがゆえに，それは〈この王国の基盤に対する内的な支えを失わしめるもの〉であると認識された。しかも，これらの逆理を招来した論法が人間理性による正確な推論の核心に触れるものであるだけに事態は深刻であり，数学における概念構成や論法についての深い反省に基づく数学の基礎づけが根本問題となって，数学基礎論という研究分野が発生した。

初期に生じた種々の立場

数学を安全な基盤のもとに基礎づけるに当たって，数学的存在，数学的事実とはいかなるものであるべきかという考えの違いから，数学基礎論発生の当初，それぞれ著名な学者によって主張されるいくつかの立場が生じ，激しい論争が行われた。歴史上〈宗派〉論争のあまりない数学において起こったこうした事態は，当時の危機意識の深さをものがたるものであろう。論理主義と呼ばれる立場に立つラッセルは，数学は論理学の1分科であるとし，逆理はさまざまな概念の〈型〉を無視するために生ずるものと主張する。実際に，A.N.ホワイトヘッドとの共著による3巻からなる大著《プリンキピア・マテマティカ》で，〈分岐した型の理論〉の記号論理の体系を建設し，その中で実数論を構成したが，その際，〈型の解消にかかわる〉還元公理という不満足なものを仮定せざるをえなかった。L.E.J.ブローエルは，数学的真理や対象は数学を考える精神とかかわりなく存在するとはせず，経験的・直観的精神活動によって直接にとらえられるものであって，実際に構成できる対象だけが数学的存在であると主張する。ブローエルが提唱した立場は直観主義と呼ばれ，この立場では排中律は一般には成り立たないものとされる。ススリンM.J.Souslinによる解析集合（ボレル集合の拡張）の発見（1917）を端緒として，ルージンN.N.LusinやシェルピンスキW.Sierpińskiらが精力的に解析集合論，一般に記述集合論と呼ばれる分野の研究に着手したのもこの時代である。彼らも明確に解析学の基礎づけをその視野の中に入れていた。E.ボレル，H.ルベーグ，ルージンらいわゆるフランス経験主義の立場に立つ解析学者もまた集合論における自由な概念構成に批判的で，とくに選択公理の使用を認めず，数学的存在としては個体的に指名できるものを具現的（エフェクティブeffective）な存在と考える。この意味で，その立場はしばしば半直観主義とも呼ばれる。

　形式主義の立場に立つ公理主義者D.ヒルベルトは楽観的な態度をとり続け，数学は何らかのくふうにより，〈そのままの形〉で救えるものと考えた。1920年代後半，彼は数学（例えば解析学）を記号論理の中で形式化して得られる公理的体系を考え，その体系の無矛盾性の証明を有限の立場で行うという基本的プログラム（ヒルベルトの計画という）を提出，みずからもP.ベルナイスの協力を得つつその実行を試みた。ヒルベルトの計画の出現以後，数学基礎論は形式主義の立場を主軸として，それぞれの立場での成果をとり入れつつ大きな発展を示した。それにはK.ゲーデルによるいくつかの仕事が決定的な役割を果たした。

証明論

ヒルベルトの計画によれば，記号論理の方法を用いて公理的体系として形式化された数学と，その形式的体系について研究する数学とを厳密に区別する。後者を超数学といい，その論法は有限的，構成的なしかたによらなければならない。超数学では体系内での証明自体が研究の主たる対象とされるからこれを証明論proof theoryともいう。与えられた形式的体系について，証明論の究極の目標は〈矛盾に至る証明はその体系内ではありえない〉ことを証明することである。さかのぼって，ヒルベルトは《幾何学基礎論》（1899）でユークリッドの《ストイケイア》の欠陥を補ってユークリッド幾何学の完全な公理系を与え，それらの公理の独立性と公理系の無矛盾性を証明した。しかし，その証明は結局実数論の無矛盾性に帰着させるもので，〈実数論が無矛盾ならば，ユークリッド幾何学もまた無矛盾である〉という相対的無矛盾性relative consistencyである。このように他の理論の無矛盾性に帰着しないような数学の各理論，とりわけ実数論の無矛盾性の証明を，いかなる疑念やあいまいさもない構成的なしかたで達成することがヒルベルトの計画であった。

　ゲーデルは，1931年に〈自然数論以上の数学的内容をもつ形式的体系がもし無矛盾ならば，その体系の無矛盾性の証明は体系内で形式化可能な方法によっては証明できない〉（ゲーデルの定理）ことを証明した。当時，ヒルベルトのいう有限の立場での超数学の実行とは，初等数論で用いられる有限的方法と同様に疑いの余地のない確かな論法で数学に矛盾のないことを証明することと解されていたので，ゲーデルによるこの結果は人間の理性一般における限界を示したものとして衝撃を与えた。しかし，ゲーデルの定理はヒルベルトの計画に重大な制限を与えたことにはなるが，その計画自体の挫折を意味するものではない。その後ヒルベルト自身も述べているように，それは有限の立場を従前の初等的にではなく，より鋭い意味で用いることが迫られることを意味している。実際に，36年にゲンツェンG.Gentzenは有限の立場を一段と深化発展させることにより算術（純粋数論）の無矛盾性を達成するという画期的な仕事を行った。

　ゲンツェンは1934年の学位論文《論理的推論の研究》において，数学で通常行われる推論をそのまま反映するような自然な論理計算の形式化を試み，それに技術的な推敲（すいこう）を行って1階の述語論理のまったく新しい形式の体系LK（ゲンツェン・タイプの体系という）を導入し，論理についてのまことに美しい法則〈LKで証明できる論理式は三段論法をまったく用いないで証明できる，すなわち，回り道のない証明を与えることができる〉（ゲンツェンの基本定理）を示したが，上述の36年の論文《純粋数論の無矛盾性》で，純粋数論をLKで形式化し，その無矛盾性を順序数ε₀までの超限帰納法によって証明したのである。ここで，ε₀とはωξ＝ξとなるような最小の順序数であって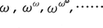，の極限数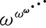である。与えられた証明図（ゲンツェン・タイプの体系での形式的な証明）にその複雑さを表す印としてε₀より小さな順序数を具体的につけ，そのしかたは次々とより簡明な証明図へと還元される過程において目前に示される証明図の列に付される順序数の列が逐次確実に小さくなっていくように与えられ，したがってそのような還元過程は有限回で完了する。こうした論法によって，矛盾へと至る証明図はありえないことが確かめられるのであって，それは構成的なものとして承認できる論法である。

　本質的に算術を超える内容をもつ実数論ないしは解析学となると，不可避的に集合概念を含むためその無矛盾性の証明は極度に困難である。竹内外史は，53年にLKを拡張して高階の述語論理をゲンツェン・タイプで形式化（GLCと呼ばれる）し，GLCに対してもゲンツェンの基本定理と同様な定理が成り立つという予想（基本予想と呼ばれる）を立て，基本予想が有限的構成的しかたで証明できれば，解析学の無矛盾性は一挙に解決されることを示した。竹内は基本予想の部分的解決を重ねるとともに，その補助手段として構成的順序数の一種であるオーディナル・ダイヤグラムordinal diagramなる概念を導入，その理論の発展と整備補強に努め，広範な内容をもつ解析学の部分体系の無矛盾性を証明した。この証明は有限の立場からはなお若干の不満はあるものの，今日まで証明論で得られている最良の結果である。なお，基本予想自体は数学的には正しいことが（非構成的手段を用いて）高橋元男とプラビッツD.Prawitzによって，それぞれ独立に証明されている。

公理的集合論

ラッセルの逆理などカントルの集合論で現れたいくつかの逆理は，あまりにも多くの要素をもつようなものを集合と考えることによって生ずるものであって，これらの逆理は，まもなく，E.ツェルメロらによる集合論の公理化によって，集合の生成原理を明確に規定することにより回避できるようになった。公理的集合論における最大の成果はカントルの集合論が出現以来の中心的課題の連続体仮説の解決であって，ゲーデルおよびコーエンP.J.Cohenに負うている。

　1908年，ツェルメロによって初めて提示された集合論の公理系は，22年にフレンケルA.A.Fraenkelによって補強され，次いでJ.フォン・ノイマンによる記号論理を用いて形式化や形式上の拡張を経て，P.ベルナイス，ゲーデルによって整備された。集合論の公理系として，ツェルメロ=フレンケルの集合論（ZFC）と呼ばれるものと，ベルナイス=ゲーデルの集合論（BGあるいはNBG）と呼ばれるものとがあるが，後者は前者の形式上の拡張であって，両者は内容的には同じものと考えられるので，以下ZFCについて述べる。

　ZFCは述語論理の記号以外には＝と∈だけの記号をもった第1階の述語論理で形式化された体系であって，その公理系は，

（1）外延性の公理　≏a≏b（≏x（x∈a↔x∈b）→a＝b），（2）空集合の存在公理　≐a≏x（x∉a）（これによって存在を保障される集合aは公理（1）によりただ一つであることが示され（以下同様），φで表す），（3）対の公理　≏a≏b≐c≏x（x∈c↔（x＝a∨x＝b））（集合a，bに対して，この公理によって規定される集合cを｛a，b｝で表し，a＝bのときは単に｛a｝とかく），（4）和集合の公理　≏a≐b≏x（x∈b↔≐y（x∈y∧y∈a）），（5）べき集合の公理　≏a≐b≏x（x∈b↔x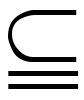a），（6）無限公理　≐a（φ∈a∧≏x（x∈a→x∪｛x｝∈a））（このような集合aの最小の集合がωであって，φを0，n∪｛n｝をn＋1とすれば，ω＝｛0，1，……，n，……｝でかつピアノの公理が成り立つことが以上の公理および後述の分出公理とから示される），（7）置換公理　≏x≏y≏z（φ（x，y）∧φ（x，z）→y＝z）を満たす論理式φ（x，y）に対して，≏a≐b≏y（y∈b↔≐x（x∈a∧φ（x，y））），（8）正則性公理　≏a（a≠φ→≐x（x∈a∧x∩a＝φ））および選択公理とからなっている。なお，公理系から選択公理をはずした体系をZFで表す。論理式φ（x）に対して，≏a≐b≏x（x∈b↔x∈a∧φ（x））を分出公理（部分集合の公理とも呼ばれる）という。分出公理はすこぶる有用であるが，これは置換公理よりは本質的に弱いものであって，集合の生成原理としては不十分である。上の公理系で置換公理の代わりに分出公理をおいた体系をツェルメロの集合論という。

　ゲーデルは1939年〈ZFが無矛盾ならば，それに選択公理（ACとかく）と一般連続体仮説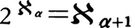をつけ加えてもなお無矛盾である〉ことを示した。いま，Aを対象領域とし，Aの要素の間には関係∈_aが定義されているような構造＝〈A，∈_a〉を考える。ZFにおける論理式φに対し〈でφが満たされる〉と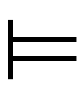きφとかき，をφのモデルという。さて，論理式φ（x）で定義されるAの部分集合｛x∈Α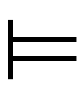｜φ（x）｝の全体をDef（A）とし，Onを順序数の全体（このようなものは集合ではなく，部類classと呼ばれる）として，L_α（α∈On）を超限帰納法により次のように定義する。

　L₀＝｛φ｝;

　αが孤立数，すなわちα＝β＋1のとき，

　L_α＝Def（L_β）;

　αが極限数のとき，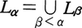

集合aがL_αの要素であるとき，aを構成可能な集合と呼び，構成可能な集合の全体をLとする。VをZFの集合の全体（ユニバースと呼ばれる）とするとき，V＝Lを構成可能性公理という。ゲーデルは，⊿＝〈L，∈〉がZFのモデルをなし，しかも⊿ではV＝Lが満たされ，かつV＝LからZFの公理だけを用いて選択公理と一般連続体仮説とが導かれることを証明したのである。ゲーデルによる簡潔にして完全な証明が《選択公理と一般連続体仮説の集合論からの無矛盾性》（1940）で与えられている。

　1963年，コーエンは強制法forcingという新しい手法を発見して，V＝L，連続体仮説や選択公理がそれぞれZFC（あるいはZF）から独立であることを示す画期的な仕事を行った。実際に，コーエンは，ZFが無矛盾ならば，（1）ωの部分集合で構成可能でない集合a，すなわち，a⊂ωでa∉Lとなるような集合aが存在し，しかも一般連続体仮説（もちろんACも）が成り立つようなZFのモデルが存在する（ゲーデルの結果と合わせ考えれば，V＝LはZFに一般連続体仮説をつけ加えたものから独立），（2）選択公理は成り立つが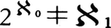，であるようなZFのモデルが存在する（したがって連続体仮説はZFCから独立），（3）ωのべき集合P（ω）がいかなる順序をつけても整列集合にはならないようなZFのモデルが存在する（したがって選択公理はZFから独立）ことなどを証明した。その後，コーエンの手法は応用上より便利な方法への言いかえや改良，拡張も多くの学者によってなされるとともに，未解決であった種々の問題がZFCと独立であることが示された。しかし，連続体問題そのもの，すなわち，連続体の濃度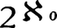は真にいかなるアレフ数であるか，は今日なお未解決であって，マルティンD.Martinの公理の提唱など，より真実を反映する公理の模索や種々の巨大濃度なる概念の研究などZFCの補強に主たる関心がはらわれている。

リカージョン・セオリー

帰納的関数の理論は有限的手法やアルゴリズムについての数学的研究に端を発したもので，エルブランJ.Herbrandの提唱に基づき，ゲーデル，クリーネS.C.Kleeneによって帰納的関数の定義が確立した（1936）。アルゴリズムや実際に計算可能といった概念についてのまったく異なった様式によるいくつかの数学的定義が同時期に提出されたが，それらはいずれも同等な概念であることが証明されたことなど種々の理由によって，〈その値を計算するアルゴリズムを有する関数とは帰納的関数のことであると解しよう〉というチャーチの提唱Church's thesisとなった。これはきわめて妥当なものと認められ，帰納的関数の理論は決定問題の解決に数学的根拠を与えることとなった。自然数の集合や自然数に関する命題P（x₁，……，x_n）がリカーシブrecursiveであるとは，その特性関数あるいは表現関数が帰納的関数となるときをいう。体系Sにおいて対象a₁，……，a_nに関する命題P（a₁，……，a_n）が与えられているとき，SにおけるPの決定問題とは，Sにおいて命題Pの対象となりうる任意のa₁，……，a_nに対し，P（a₁，……，a_n）が成り立つかどうかを有限回の操作で判定する一様な手順を求めることである。通常，数学の体系は記号はたかだか可算個であり，その対象は記号の有限列であるから，ゲーデル数を用いてSを算術化することができ，したがってPを自然数に関する命題とみなすことができる。Pがリカーシブでないとき，SにおけるPの決定問題は否定的に解かれたという。群の語の問題などいくつかの決定問題が否定的に解かれたが，もっとも大きな成果はヒルベルトの第10問題（整係数の不定方程式が有理整数解を有するかどうかを判定する一般的手順を求めよ）が否定的に解決されたことである（1970）。

　チャーチの提唱に基づいて在来の解析集合論を見直すとき，いわゆる半直観主義の数学でいうエフェクティブの概念は帰納的関数を用いることにより，かなり透明なものとなった。さらにクリーネの寄与に負うリカージョン・セオリーの発展に伴って，在来の記述集合論を含む統一的な理論として記述集合論を再展開することが可能となり，公理的集合論の発展とあいまって，記述的集合の濃度の問題やルベーグ可測性の問題など，1930年代未解決として残されていた諸問題のいくつかが解決され，記述集合論の隆盛をみることとなった。他方，ハイティングA.Heytingによる直観主義論理の形式化（1930）やゲーデルの解釈によって，直観主義の立場で用いられる論理が明確なものとなったが，帰納的関数を用いての直観主義的数学の合理化がクリーネによって試みられたのを契機として，直観主義の立場からの研究は構成的数学constructive mathematicsの研究とともに盛んに行われている。

　なお，A.タルスキーやロビンソンA.Robinsonをそれぞれ中心とする学派で盛んに研究されてきたモデル論model theoryは，今日数理論理学における重要な分野として発展しているのみならず，公理的集合論をはじめ数学基礎論の各分野で有効な役割を果たしている。もともと構文syntax的研究の立場に端を発しているリカージョン・セオリーにおいても，その対象が一般化（例えば順序数上の帰納的関数や帰納的汎関数など）されるに伴って，意味論semantics的研究にその端を発するモデル論的手法が有効に用いられている。また，モデル論の重要な成果として，ロビンソンが創始（1961）した超準解析non standard analysisを挙げておかねばならない。
執筆者：柘植 利之

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

数学基礎論
すうがくきそろん

数学の基礎に関する数学的理論のことである。19世紀に導入された集合論は、ただちに逆理を発生させたにもかかわらず、他方では数学における基本的で有用な概念であることが漸次認められるようになった。この逆理の解明と除去が動機となって、数学の認識の本質、論理学と数学との関係などが論究され、数学の論理的構造、数学の証明に使われる論理への反省が全般的に論じられるようになり、三つの立場が生じた。すなわち、B・A・W・ラッセルの論理主義、ヒルベルトの形式主義、ブラウアー（ブローエルともよばれる）Luitzen Egbertus Jan Brouwer（1881―1966）の直観主義である。

　論理主義では、数学を論理学の一分科であると考え、記号論理の形で数学を再構成することを試みた。これはA・N・ホワイトヘッドと連名の大著『プリンキピア・マテマティカ』Principia Mathematica全3巻（1910～1913）に集大成された。形式主義では、数学を記号論理の方法で形式化し、数学の証明そのものを、意味をもたない記号列の変換と考え、これを数学的対象とし、その形式化された数学の公理系の無矛盾性を証明しようとした。形式化された数学を対象とする数学を、形式化された数学と区別して、超数学あるいは証明論という。直観主義では、数学的真理や対象が、数学を考えていく意味や内容によって直接にとらえられるものであるという考えにたち、証明に用いる論理でも、排中律（命題については、真か偽かの二つの場合しかないとする法則）を普遍的に正しい法則としては認めない立場をとった。

　これらの三つの立場は、激しい論争を経ながら、互いに他に影響しあい、今日の数学基礎論へと発展した。まず、G・カントルの集合論はツェルメロ（1908）、フレンケルA. A. Fraenkel（1922）によって公理化され、J・ノイマン（1927）、ベルナイズP. Bernays（1936）によって整備された。ゲーデルは、集合論発生以来の問題であった連続体仮説が他の公理と矛盾しないことを証明した（1938）。さらにR・J・コーエンは連続体仮説の否定も他の公理と矛盾しないことを示し（1963）、連続体問題が集合論の公理系から独立であることが示された。証明論では、自然数論の無矛盾性がゲンツェンG. Gentzenによって証明された（1936）。また、自然数論を含む形式的体系は、その形式的体系のなかでは肯定も否定も証明できない（決定不能）命題を含み、さらに「形式的体系が無矛盾である」ことがその形式的体系のなかでは証明できない、という不完全性定理がゲーデルによって示され（1931）、解析学、公理的集合論の無矛盾性を証明論の立場から証明することの困難さが示された。この方向は、チャーチAlonzo Church（1903―1995）やクリーニStephen Cole Kleene（1909―1994）による帰納的関数（1936）、チューリングによるチューリング機械（1936）によって、計算可能という概念が確立するとともに、計算の理論へと発展し、今日では情報科学と密接に結び付くものとなった。

　また、形式的体系は直観主義体系、多値論理や様相論理などを包括するようになった。また、形式的体系の記号に対する集合論的意味づけを通して、各種の理論が展開されている。この方面の最初の成果はゲーデルによる完全性の定理（1930）であり、今日ではモデルの理論として大きく発展している。

［西村敏男］

[参照項目] | 形式主義 | 直観主義 | 論理主義

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

数学基礎論
すうがくきそろん
foundation of mathematics

20世紀初頭に始った，数学の基礎に関する諸理論をさし，現在では数学の一分科となっている。数学は G.カントルの集合論によって飛躍的な進歩をみたが，それは同時に逆理を導くことも明らかになった。形式論理の問題ともいえるこのような数学上の逆理を解決するために，数学の基礎への反省が，多くの数学者を数学基礎論に着目させる動機となった。数学の本質をどう把握するかによって次の3つの立場があった。 (1) 論理主義　イギリスの B.ラッセルを中心として主張された。数学を論理学に含めようとするもので，1930年代にアメリカの K.ゲーデルによってこの試みが失敗であることが証明されたが，記号論理学という分科が，現在でもすぐれた役割を果している。 (2) 直観主義　オランダの L.ブローエルの説をさしていう。数学的存在や真理は，それ自体独立に存在するものではなく，人間精神の構成的直観によって直接把握されるものであるという主張。ただし現在では，排中律を除いた論理と理解されている。 (3) 形式主義　ドイツの E.ツェルメロ，D.ヒルベルトらによって代表される立場。数学における「存在」とは，単に「無矛盾性」を意味するにすぎないと主張する。しかしながら，これもゲーデルらによってヒルベルトの考えどおりには実現できないとみられている。ゲーデル以後，数学基礎論は，数学の一分科として独立し，数学自体を対象化したものとなり，いろいろな「集合論」が考察の対象となるようになった。直観主義も，ブール束に基礎をおく古典論理と違った，もっと広い直観主義論理による形式として，各種の中間論理の一つの形で定式化される。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

数学基礎論【すうがくきそろん】

数学の基礎に関する数学的理論。カントルが創始した集合の概念から重大なパラドックスを生じたことから，数学の概念構成法，論法について反省が加えられて成立，発展。数学を論理学の一分科とみなす論理主義（B.ラッセルら），数学の真理や対象は精神活動によって直接とらえられるとする直観主義（L.ブローエルら），論理や集合論的方法も含めて数学を公理化し，形式化された公理系の無矛盾性を証明することによって数学基礎論の問題を解決しようとする形式主義（D.ヒルベルト，K.ゲーデルら）などの立場がある。
→関連項目形式主義｜集合論｜フォン・ノイマン

出典　株式会社平凡社

世界大百科事典（旧版）内の数学基礎論の言及

【フレーゲ】より

…フレーゲは論理主義の放棄を強いられ，晩年には算術の真理を総合的なものとする立場から再度基礎づけを試みた。このように，現代の数学基礎論，論理学の基礎を築いただけでなく，厳密で形式的に隙のない体系を求めて営まれた記号，言語に関する考察は，現代の言語理論の出発点となっている。ウィトゲンシュタインの思索はその圧倒的な影響下にあり，また，同時代の主流であった心理学主義的，形式主義的，物理主義的な数学論，意味論を批判して，言語使用を人間的行為としてとらえその中で記号の意味とそれが指し示すものを区別する意味論を提出した。…

※「数学基礎論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」