置換積分法（読み）ちかんせきぶんほう

改訂新版　世界大百科事典

置換積分法 (ちかんせきぶんほう)

関数f（x）の不定積分を求めるのに，x＝φ（t）により積分変数xをtで置き換えて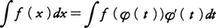，として計算することを置換積分法という。定積分の場合は，φ（t）が区間α≦t≦βで微分可能な増加関数であって，φ′（t）がこの区間で積分可能ならば，a＝φ（α），b＝φ（β）とするとき，a≦x≦bで積分可能な関数f（x）に対して次の公式が成立する。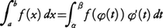

　2変数の関数の場合は，適当な滑らかさの条件を満たす関数x＝φ（u，v），y＝ψ（u，v）によって，（x，y）平面の領域Aと（u，v）平面の領域Bとが1対1に対応するならば，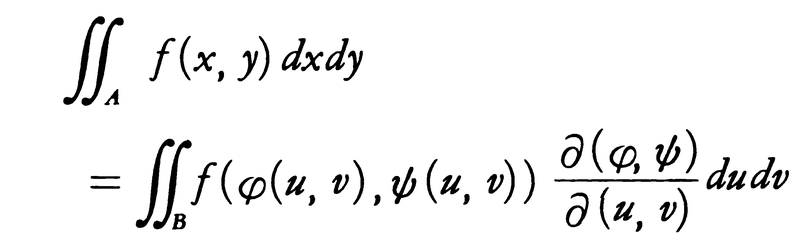

ここに，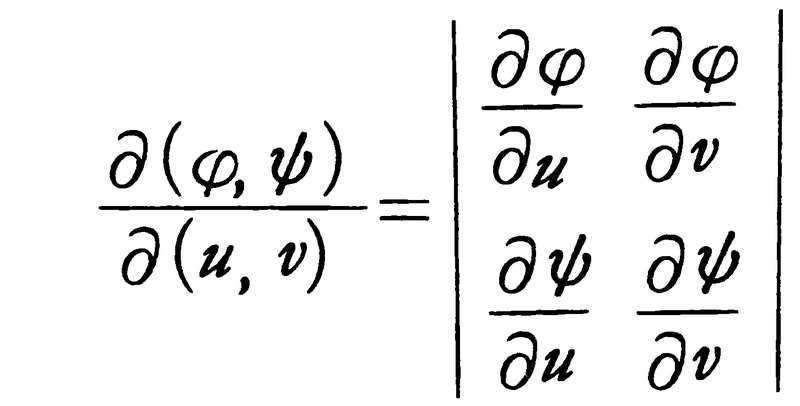

であって，この行列式はφ，ψのu，vに関する関数行列式，またはヤコビの行列式と呼ばれる。例えばA＝｛（x，y）｜x²＋y²＜a²｝のとき，x＝rcosθ，y＝rsinθによって直交座標（x，y）を極座標（r，θ）で置換すると，AはB＝｛（r，θ）｜0≦r≦a，0≦θ＜2π｝に1対1に写され，関数行列式＝rとなり，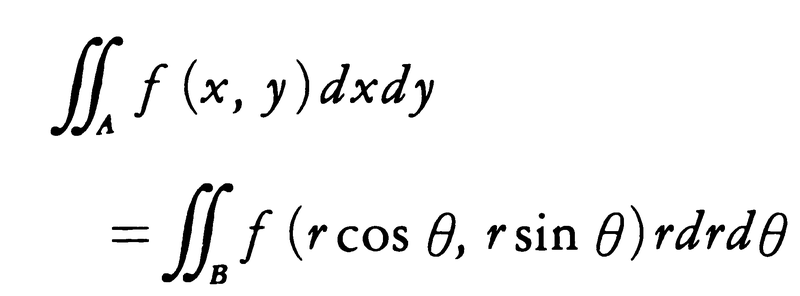

となる。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の置換積分法の言及

【積分】より

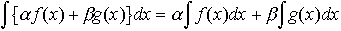…ただし不定積分を含む等式は，定数の差を除いて成り立つのである。(1)線形性　α,βを定数とするとき，(2)部分積分法　f,f′，g,g′が連続ならば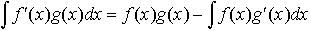，(3)置換積分法　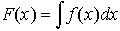においてx＝φ(t)(ただし，φの値域はfの定義域に含まれ，φ′は連続とする)とおくと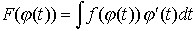，とくにφが狭義単調ならば，連続な逆関数φ^－1が定まり，上の式の右辺を計算してからt＝φ^－1(x)を代入して，f(x)の原始関数F(x)が求められる。　次に初等関数の不定積分を与える公式のおもなものを表に列挙する。…

※「置換積分法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」