改訂新版 世界大百科事典 「逐次近似法」の意味・わかりやすい解説
逐次近似法 (ちくじきんじほう)
successive approximation
方程式を解くに当たって,最初一つの近似解を推定し,次にこの近似解を用いてさらに精度のよい近似解を求め,逐次この操作を繰り返して近似の精度を高める方法を逐次近似法という。この操作を無限に繰り返したとき近似解が一つの極限に収束するならば,それは実際の解になる。したがってこの方法を用いて解の存在を証明することができるし,また数値解法の手段としても利用できる。
常微分方程式x′=f(t,x)において,t=aでx=bとなる解をx(t)とすれば,これは積分方程式,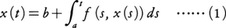
を満足する。このことを利用するとピカールC.E.Picardの逐次近似法,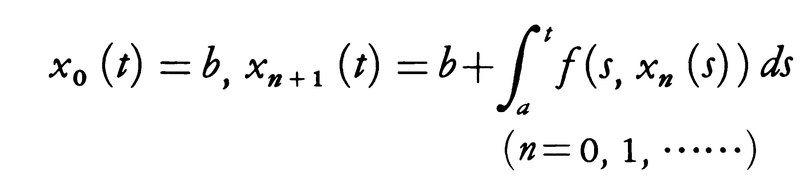
が得られる。f(t,x)がtおよびxについて連続であり,xについてリプシッツの条件Lipschitz's condition|f(t,x)-f(t,x′)|≦L|x-x′|を満たすならば,この逐次近似公式から得られる関数列{xn(t)}は(1)の解x(t)に一様収束する。このことによって常微分方程式の初期値問題の解の存在を証明することができる。
ボルテラV.Volterraの積分方程式,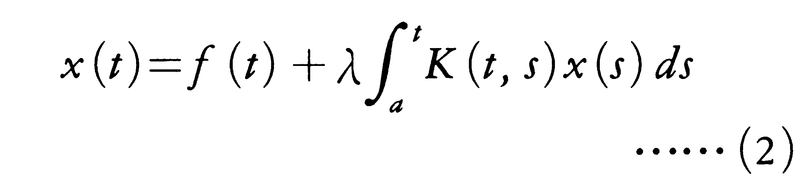
において,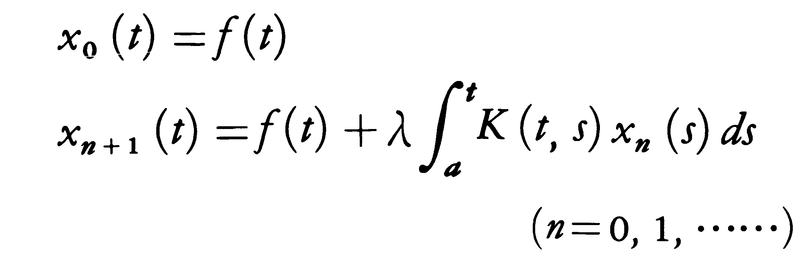
とする。K(t,s)がa≦s≦t≦bにおいて連続ならば,この逐次近似関数列{xn(t)}はa≦t≦bおよび任意のλに対して(2)の解に一様収束する。これはピカールの逐次近似法の特別な場合である。このとき反復核Kn(t,s)を,
によって定義すればxn(t)は具体的に,
と書くことができる。
フレッドホルムE.I.Fredholmの積分方程式,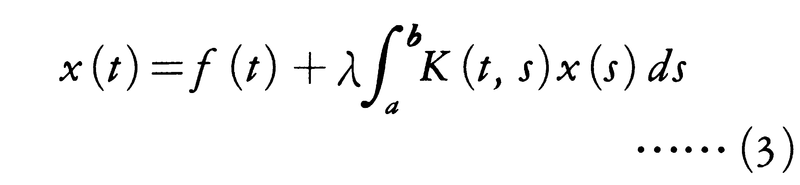
において,
とする。K(t,s)がa≦t≦b,a≦s≦bにおいて連続であり,その範囲で|K(t,s)|<Mとすれば,この逐次近似関数列{xn(t)}は,a≦t≦b,|λ|<M⁻1(b-a)⁻1において(3)の解に一様収束する。なお,反復核Kn(t,s)を,
によって定義すれば,xn(t)は具体的に,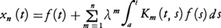
と書くことができる。
これらはいずれも,解の存在を証明するための方法として用いられる逐次近似法であって,数値解法として利用するには必ずしも適当な方法ではない。近似解が真の解に収束する速度が必ずしも速くないからである。数値解法のためには,いろいろな場合について,それに適した逐次近似法が考案されている。微分方程式に対するルンゲ=クッタの方法Runge-Kutta method,ガレルキン法Galerkin's methodなどがそれである。
執筆者:斎藤 利弥
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

