一様収束（読み）いちようしゅうそく（その他表記）uniform convergence

日本大百科全書(ニッポニカ)

一様収束
いちようしゅうそく
uniform convergence

関数の列f₁(x),f₂(x),……や、関数を項とする級数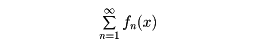

が収束する状況を示す術語。

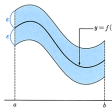
　関数g(x)が関数f(x)に近いというのは、常識的には、図Aのようにy=f(x)のグラフを中心として上下に小さな幅εの帯を考えたとき、y=g(x)のグラフがこの帯のなかに入ってくることと考えられる。このように、考察している範囲内のどのxについても同様の近さで収束していくのが一様収束である。これは、単に各点で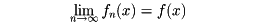

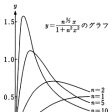
が成立しているというだけでは実現されない。関数列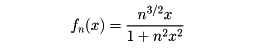

では、各点でゼロに収束するけれども、図Bに示すように、見た目にはそのような印象は得られない。この一様収束が重要な理由は、次の定理が成立するためである。(1)連続関数の一様収束極限は、また連続関数である。(2)関数列が一様収束すれば、極限関数の積分は、各関数の積分の極限に等しい。つまり、一様収束f_n(x)→f(x)のとき、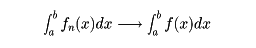

　なお、関数項級数の一様収束は、その部分和の列の一様収束で定義されるが、これを判定するための次の定理はきわめて有用である。

［竹之内脩］

ワイエルストラスの優級数定理

関数項級数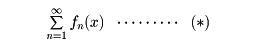

があり、すべてのxについて、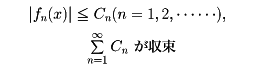

が収束を満足する数列｛C_n｝が存在すれば、（＊）は一様収束である。

［竹之内脩］

[参照項目] | 収束

一様収束説明図〔図A〕

一様収束説明図〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

一様収束
いちようしゅうそく
uniform convergence

実変数の関数列 f₁(x) ，f₂(x) ，…，f_n(x) が閉区間［ a ，b ］で定義されているとき，この区間のすべての変数 x に対して，n→∞ のとき，関数列 {f_n(x)} の極限値 (極限関数) (x) が存在すれば，この関数列は区間［ a ，b ］で収束するというが，そのとき f_n(x) と f(x) との差の限界が n に依存する可能性がある。これが n について一様に小さくできるとき，すなわち，任意の整数 ε に対して，x に無関係な数 n₀ が存在し，n＞n₀ を満足するすべての n に対して，区間［ a ，b ］で，｜f_n(x)－f(x)｜＜ε となるとき，関数列 f₁(x) ，f₂(x) ，…，f_n(x) は区間［ a ，b ］で f(x) に一様収束するという。また，実変数の級数についてはその部分和の関数列が，ある集合 D で一様収束すれば，この級数は集合 D 上で一様収束するという。複素変数関数の一様収束級数は，実変数の場合と同様にして定義することができる。その性質も同じである。

出典　ブリタニカ国際大百科事典 小項目事典