デバイの特性温度（読み）デバイノトクセイオンド

化学辞典 第2版

デバイの特性温度
デバイノトクセイオンド
Debye characteristic temperature

固体のモル熱容量に関するデバイの理論で導入した温度で，この温度以下では固体のモル熱容量はデュロン-プティーの法則からはずれる．A. Einstein(アインシュタイン)の理論で，固体のモル熱容量が低温で T ³ 法則(Tは絶対温度)に従わないのは振動数νをただ1種類と仮定したためである．低温では固有振動は小さな振動数のものが重要となるので，振動は固体を伝わる弾性波として扱ってよい．振動数がνとν＋dνの間にある固有振動の数は，

g(ν)dν ＝ 4πV(c_l^－3 ＋ 2c_t^－3)ν ²dν

を与えられる(Vは固体の体積．c_l，c_t はそれぞれ縦波，横波の速度)．この式は，νがあまり大きくないときに正しい．固有振動の総数は自由度 3N(Nは原子の総数)に等しいとすると，最大の振動数 ν_m が存在する．Einsteinの理論での特性温度 θ_E に対応して，温度(θ_D)を定義し，これをデバイの特性温度またはデバイ温度という．

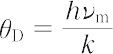
ここで，hはプランク定数，kはボルツマン定数．モル熱容量は，

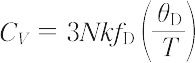
で与えられ，これをデバイのモル熱容量式という．低温で T ³ 法則を与え，しかも温度の全域にわたって固体のモル熱容量をよく説明する．ここで，

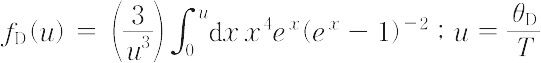
で，デバイ関数とよばれる．[別用語参照]アインシュタインの比熱容量式

出典　森北出版「化学辞典（第2版）」