アインシュタインの比熱容量式（読み）アインシュタインノヒネツヨウリョウシキ

化学辞典 第2版

アインシュタインの比熱容量式
アインシュタインノヒネツヨウリョウシキ
Einstein's formula for specific heat capacity

固体の比熱容量C_V は，絶対温度Tが0に近づくと，T ³ に比例して0に近づき，デュロン-プティーの法則

(C_V ＝ 3NR ＝ 25 J K^－1 mol^－1 は物質によらず一定)
からいちじるしくはずれる．A. Einstein(アインシュタイン)は1907年に量子論にもとづいて，固体の比熱容量は低温で小さくなることを理論的に導いた．かれは T ³ 法則までは出せなかったが，1912年，P.J.W. Debye(デバイ)がその導出に成功した．Einsteinの理論は，固体を構成するN個の原子は互いに無関係に同一の振動数νで振動しているという仮定の上に立っている．量子論によると，1方向の振動のエネルギーは原子当たり，

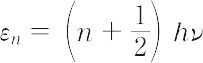
で与えられる(hはプランク定数，nは量子数)．その平均値は，

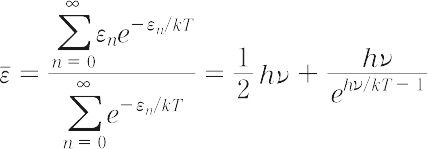
のように計算される(kはボルツマン定数)．したがって，振動の全エネルギー

U ＝ 3N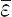
から，比熱容量は，

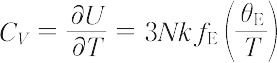
と表される．この式をアインシュタインの比熱容量式という．ただし，

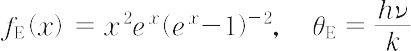
前者はアインシュタイン関数，後者はアインシュタインの特性温度とよばれる．高温(T ≫ θ_E)では

C_V ≅ 3Nk
となってデュロン-プティーの法則を説明し，低温では

C_V ≅ 3Nk(θ_E/T)²e^－θ_E/T
となってT→0で比熱は0に近づく．[別用語参照]デバイの特性温度

出典　森北出版「化学辞典（第2版）」