原子（読み）ゲンシ（英語表記）atom

デジタル大辞泉

げん‐し【原子】

１ 物質の基本的構成単位で、化学元素としての特性を失わない、最小の微粒子。原子核とそれを取り巻く1個または複数個の電子からなり、大きさは約1億分の1センチ。
２ 「原子核」「原子力」「原子爆弾」などをさす語。
[類語]粒子・分子・原子核・原子団・アトム・イオン・素粒子・電子・陰電子・陽電子・陽子・中間子・中性子・光子・エレクトロン・プロトン・ニュートロン・ニュートリノ

出典　小学館

精選版 日本国語大辞典

げん‐し【原子・元子】

1. 〘 名詞 〙 事物を構成する最後の微小存在。哲学でもいうが、特に物理化学では、物質が化学的性質を保つことのできる最小単位の粒子。半径約 10^-10 メートル。原子核といくつかの電子からなる。二つ以上が結合すれば分子をつくる。現在までに一〇三種が発見されている。〔哲学字彙（1881）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

原子 (げんし)
atom

物質の基本的な構成要素。もともとはこれ以上分割できない恒常不変な最小のものと考えられていたが，20世紀初期に原子核と電子とから構成されていることが明らかにされた。また，原子内の状態もいろいろに変わりうることがわかり，その後，さらに原子核が陽子と中性子とから構成されていることも明らかとなった。高速の原子核をもう一つの原子核に衝突させると，それらの原子核が壊れて他種の原子核に変わることもある。このように，今日では原子は厳密な意味では究極的な粒子とはいえない。

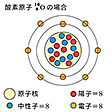
　自然に存在する物質は92種類の原子からなるが，原子にはこのほか人工的につくられる寿命の短い原子十数種の存在が確認されている。原子はほぼ球形で，その半径は10⁻¹⁰mの程度である。原子の中央には原子核があり，そのまわりに何個かの電子が存在する。原子核もほぼ球形で，その半径は10⁻¹⁵～10⁻¹⁴mの程度である。電子は原子核に比べてはるかに質量が小さいので，原子の質量はほぼ原子核の質量である。原子核は陽子と中性子とからなり，陽子の質量と中性子の質量とはほぼ等しいので，原子核の質量は陽子あるいは中性子の質量に陽子と中性子との個数の合計をかけたものに近い。陽子と中性子との個数の合計を原子核の質量数と呼び，Aで表す。陽子の電荷をeとすれば，電子の電荷は－eであり，中性子は電荷をもたない。原子核の中の陽子の個数をZ，中性子の個数をNとすれば，Z＋Nが質量数Aである。原子核の電荷はZeであり，そのまわりにZ個の電子が存在するので，原子は電気的に中性である。

　原子には水素，酸素などの名称がある。これらの名称は原子の存在が確認される以前から，元素の名称として用いられていた。元素とは2種類以上の物質に分けることのできない物質である。原子の種類を指定するのに，陽子の個数Zを用いることがあり，その場合，Zを原子番号と呼ぶ。例えば，水素原子ではZ＝1なので原子番号は1，酸素原子ではZ＝8なので原子番号は8である。

　電荷数Zが等しくて，質量数Aが異なる原子核を同位核と呼び，そのような核をもつ原子を同位体（アイソトープ）と呼ぶ。同位体は化学的にはほとんど同じ性質をもつので，同じ元素名で呼ばれる。同位体を区別するには元素記号の左肩に質量数をつけて¹⁶O，¹⁷Oのように表す。多くの同位体は放射性を示す。

　原子内の電子が1個，あるいは2個以上放出されると正イオンになり，逆に中性原子に電子がとりこまれると負イオンになる。また，一般に2個以上の原子が結合すると分子になる。イオン，分子などの中の電子の状態は中性原子の中の電子の状態と同じではないが，原子の内側の部分にはあまり変化はなく，外側の部分が化学結合に関与する。原子を原子番号の順に並べると，化学的に類似した性質をもつ原子がある周期で現れる。これを周期律と呼ぶ。周期表で同族の原子は外殻の構造が似ており，そのために類似した化学的性質を示すのである。同位体は周期表では同じ位置におかれる。

　原子内の電子と原子核とを質点と見れば，これらは一つの質点系を構成し，ニュートン力学によれば，重心運動と相対運動とは分離されるので，原子内の電子の運動を調べるには，重心が静止している場合を考えれば十分である。電子に比べて原子核ははるかに質量が大きいので，原子の重心の位置はほとんど原子核の位置と一致する。ゆえに重心が静止しているということは原子核が静止しているということとほとんど同じであり，そのまわりを電子が回転する。これは太陽のまわりを地球，火星，土星などが回っているのと似ている。しかし，実際は電子は質点ではなく，波の性質をもつことが結晶による電子線の回折現象によって明らかになり，したがって，原子内の電子の状態を記述するにはニュートン力学では不十分で，量子力学が必要になる。量子力学によると，原子内では電子は電子雲の状態で存在する。すなわち，一つ一つの電子がそれぞれ雲のように広がっている。ニュートン力学と量子力学との間にはかなりの対応関係があり，量子力学の理論の本質を理解するのにニュートン力学が役だつ場合が多い。このため，原子内で電子が円軌道や楕円軌道を描いて運動しているという描写も，一つの有用な原子模型といえる。

原子の存在の確定と原子構造の探究

物質を細分していくと，いくらでも細分できるのか，それとも，それ以上分割できない最小単位，すなわち原子に到達するのかということについては，古代ギリシアのころから論ぜられていた。デモクリトスは物質は原子からなるという原子説を唱え，アリストテレスは連続説を唱えた。しかし，この時代の議論は哲学的な推理の域を出ず，その存在が確かめられたのは近代になってからである（原子論）。1800年ころにJ.ドルトンは倍数比例の法則を発見した。それによると，2種類の元素が何種類かの化合物をつくるときに，一方の元素の一定量と化合する他方の元素の質量の比は簡単な整数比になる。倍数比例の法則は，物質が一定の質量をもつ微粒子，すなわち原子からなると考えると，合理的に理解できる。このため，倍数比例の法則は原子説の有力な根拠となった。さらに気体を密封して加熱したり圧縮したりするときに気体が示す圧力は，気体分子運動論によってみごとに説明され，このことによって，原子の実在を疑う余地は小さくなった。

　20世紀の初期に，陰極線の実験によって電子の存在が知られ，この実験によっていろいろの物質から電子が飛び出すことがわかったので，原子が実在するとすれば，電子は原子の構成要素の一つであろうと考えられるようになった。さらに，原子スペクトルなどを手がかりとして，原子の構造がしだいに明らかにされ，原子の実在は確定的となった。今日では結晶内に原子が並んでいるようすを電子顕微鏡で写すことができる。

原子核の存在

電子が発見されたころから，原子の構造を探究することが大きな問題となった。原子は電気的に中性であるから，電子が原子の構成要素の一つであるとすると，原子内にはほかに正電荷をもった構成要素が存在しなければならない。J.J.トムソンは1903年に，球状に分布した正電荷の中で，電子が一つの円周上に等間隔に並んで回転しているという原子模型を提出した。これに対し同年，長岡半太郎は，電子が正電荷の外で土星の輪のようになって回っているという原子模型を提出した。その後11年，E.ラザフォードは，α線が金属箔で散乱される際に非常に大きく方向の変わるものがあることに注目した。α粒子が原子の中に入ったとき，電子は軽いのでα粒子に飛ばされ，したがってα粒子は電子によってはほとんど曲げられない。α粒子は主として原子内の正電荷によって曲げられる。ところが，もし正電荷がある程度以上の広がりをもっていると，α粒子はその広がりの外でも，また中でも，とくに大きな力を受けず，したがってα粒子の進路はあまり曲がらないことになる。実際には，大きく進路の曲げられるα粒子があるので，このことから正電荷はほとんど広がりをもたないことが明らかにされ，この点電荷に近い正電荷の部分は原子核と呼ばれるようになった。

ボーアの水素原子模型

水素原子の発光スペクトルに著しい規則性のあることは，19世紀末から20世紀初期にかけてJ.J.バルマーらにより発見されていた。すなわち，水素原子のスペクトル線の波長λは，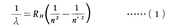

という公式で表される。ただし，R_hは水素原子のリュードベリ定数，n，n′は整数である。

　1913年にN.H.D.ボーアは上記の水素原子のスペクトルの規則性を説明するために，水素原子の構造について次のような理論を立てた。水素原子は1個の電子と1個の陽子（すなわち水素原子核）とからなる。ボーアは電子が陽子のまわりに等速円運動をしていると仮定した。電子の質量をmとし，円の半径をr，回転の角速度をωとすれば，遠心力はmrω²となる。一方，電子と陽子との間のクーロン引力はe²/r²である（原子の理論では非有理化単位系を用いることが多いので，ここではそれに従う）。遠心力とクーロン力とがつりあうとすると，mrω²＝e²/r²となる。電子の角運動量はmωr²であるが，ここで，試みに，電子の角運動量がħ（ħはプランクの定数hを2πで割ったもの）の整数倍でなければならないという量子条件を課すると，mωr²＝nħとなる。ただし，n＝1，2，3，……で，量子数と呼ばれる。上の二つの式から，r＝n²ħ²/me²となり，電子の速さはv＝ωr＝e²/nħとなる。これから，電子の運動エネルギーは1/2mv²＝me⁴/2n²ħ²となり，クーロン力の位置エネルギーは－e²/r＝－me⁴/n²ħ²となる。これを加えあわせると，量子数nの状態の電子のエネルギーとして－me⁴/2n²ħ²を得る。しかし，厳密には陽子が静止しているとしたのは正しくないので，この点を補正すると，量子数nの状態の電子のエネルギーは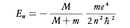，となる。Mは陽子の質量である。

　量子数n′の状態からn（ただしn′＞nとする）の状態に遷移するときに放出される光の振動数をνとし，その際に放出される光は1個の光子として放出されるものとすると，光子のエネルギーはhνであるから，エネルギー保存則によりE_n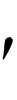－E_n＝hνでなければならない。光速度をcとすると，光の振動数νと波長λとの間にはνλ＝cという関係があるので，上式は，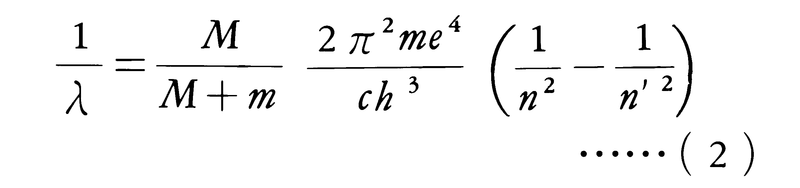

となり，ちょうど前記の波長の公式（1）式と同じ形になる。さらに，（2）式の右辺のかっこの外の部分は，ちょうど（1）式のR_hに等しい。このようにボーアの理論は水素原子のスペクトルの線の振動数を正しく与えることに成功したので，理論の目的は達成された。

　A.J.ゾンマーフェルトはボーアの理論を他の原子に拡張し，また，相対性理論も考慮に入れた。しかし，原子の正しい記述には，電子の波動性を内含する理論，すなわち量子力学が必要であり，この点でボーア，ゾンマーフェルトの理論は不完全である。ゆえにボーアの理論はボーアの原子模型と呼ばれる。

量子力学と原子

電子の波動性

電子は粒子であるが，波動性を示すことが結晶による電子線の回折で明らかになった。このことから，電子は固い粒ではなく，変形しうるものであり，一般にある程度の広がりをもっていて，その広がりの中には波があると考えることが必要になった（電子の広がりは原理的にはいくらでも大きくなりうるものであるが，その広がりの状況は直接観測にかかるものではなく，また，電子の位置を測定すると，電子は1点に収縮する）。もちろん，電子がブラウン管の中などで運動する場合は，電子は電荷をもった質点として扱ってさしつかえない。しかし，原子のような小さな世界での電子の運動を考察する場合には，電子の広がりを無視することは正しくない。すなわち，原子内ではおのおのの電子がそれぞれ雲のように広がった状態になっていることが重要な意味をもつ。この電子の雲は電子雲と呼ばれ，その中には波がある。

　ところで，われわれの日常生活において身辺にいろいろの波があるが，それらの波と電子の波（電子雲の中の波）とはある点で似ており，また，ある点では異質である。例えば，水面上の平面波はsin（kx－ωt）という関数で表され（k＝2π/λ，ω＝2πνで，λは波長，νは振動数，xは位置座標，tは時刻），また，電磁波も同じ形の関数を用いて記述されるが，量子力学によると，電子の場合，波の進行方向にx軸をとると，平面波（三次元空間の平面波）の状態はexp｛i（kx－ωt）｝という複素関数で表される。この形の複素関数は電磁波の理論でも用いられないわけではないが，それは計算技術上の目的で用いられるのであって，実体的な意味をもっているわけではない。それに対して，電子の波を表す複素関数は，量子力学によると，その絶対値の2乗が電子の密度（正確には存在確率の密度）を表し，この点で，実体的な意味を備えている。

　もっとも上記の平面波exp｛i（kx－ωt）｝は全空間に広がっているので，現実の電子の状態を表すものとはいえない。現実の電子の状態は空間の有限領域だけに波の存在する状態であって，そのような波は波束と呼ばれる。電子に力が働かないときは，このような波束は等速直線運動をし，これを粒子として観測すると，その運動量はp＝ħk，速度はv＝p/m，エネルギー（運動エネルギー）はE＝1/2mv²となる。なお，ωとEとの間にはω＝E/ħという関係があることが知られている。

　水素原子において，陽子（原子核）から十分に離れたところに上述のような電子の波束をおくと，この場合は波束は陽子からの力の影響を受けて曲線運動を行い，その曲線運動は電子を質点とした場合の運動とほぼ同じものになる。しかし電子の波束が陽子に重なるようにおかれると，その後の波の動き方は簡単には描写できない。この場合は，電子雲の各部分と陽子との間の距離がそれぞれ異なるので，古典力学（ニュートン力学）との類似性が希薄になる。このような場合を含めて，一般に電子の状態は一つの波動関数ψ（x，y，z，t）で表される（x，y，zは位置座標）。管の中で空気を振動させると定常波が生ずることがあるが，量子力学によれば，原子内の電子の波についても定常波があり，定常波が存在するときその状態を定常状態と呼ぶ。水素原子のような1電子系の場合，定常状態の波動関数ψ（x，y，z，t）はψ（x，y，z，0）・exp｛－iEt/ħ｝の形をもつ（ここでEはその状態の電子のエネルギーである）。空気の振動の定常波の振動数がとびとびの値をとるのと同様に，原子内の電子の定常状態のエネルギーEもとびとびになっている。定常状態の波動関数は上記の形をもつので，電子の密度｜ψ（x，y，z，t）｜²は時間によって変化しない。なお，Eは原子の中に存在するエネルギーであるから，原子のエネルギーと呼んでもよい。

量子力学による水素原子の理論

水素原子の定常状態の波動関数とそのエネルギーとは，量子力学によって正確に求まり，このようにして定まる水素原子のエネルギー準位は，ボーアの原子模型で求められたエネルギー準位と正確に一致する。水素原子の基底状態（もっともエネルギーの低い定常状態）は後に述べる理由で1s状態と呼ばれ，その波動関数は，時刻tに依存する因子exp｛－iEt/ħ｝を除いて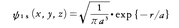，と表される。ただし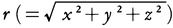，は原点（陽子の位置）からの距離を表す。aはボーアの原子模型におけるn＝1の円軌道の半径，すなわち，a＝ħ²/me²であり，ボーア半径と呼ばれる。その値はa＝0.53×10⁻¹⁰mである。なお，1s状態の電子雲は原点のまわりに球対称に分布しており，その広がりは半径aの程度であるが，電子雲と原点との間の距離rの平均値はaには等しくない。これに対して，1/rの平均値はちょうど1/aになる。

　量子力学によれば，1s状態の電子のエネルギーは，ボーアの原子模型のn＝1の状態のエネルギーと一致する。1sの1はn＝1を意味する。ところで，ボーアの原子模型ではnは角運動量に関連した量子数であったが，この点については再考を要する。すでに述べたように，電子の波束と陽子とが十分に離れている場合には，古典力学と量子力学との区別が小さく，角運動量の概念も古典力学と量子力学とに共通であるが，上記の1s状態のように電子雲が陽子に重なっている場合は，古典力学と量子力学との対応がよくない。量子力学によれば，上式のような球対称な状態では角運動量は0である。一般に定常状態は定常波の状態であり，定常波には腹と節とがあって，節のいくつかは同心球面である。量子力学においては，同心球面以外の節面の個数lは角運動量の大きさを表す量子数である。また，節面の総数に1を加えたものがちょうどボーアの原子模型の量子数nに等しい。このように，量子力学とボーアの原子模型とは完全には対応しない。すなわち，ボーアの原子模型ではn＝lの状態を考えていることになるが，量子力学ではn＞lの定常状態しか存在しない。nは主量子数，lは角運動量量子数，あるいは方位量子数と呼ばれる。lが0，1，2，……の状態を，分光学的な起源をもつ記号s，p，d，……で表す慣習があり，1sのsはこれによるものである（これについては〈原子スペクトル〉の項目に詳しく述べてある）。

　基底状態以外の定常状態は励起状態と呼ばれ，とくに，エネルギーのもっとも低い励起状態は第一励起状態と呼ばれる。水素原子の第一励起状態のエネルギーは，ボーアの原子模型のn＝2の状態のエネルギーと一致する。量子力学では，このエネルギー準位に2s，2p1，2p0，2p－1の4種類の状態がある。2s，2p1，2p0，2p－1の2はn＝2を表し，s，pはそれぞれl＝0，1を表す。また2p1，2p0，2p－1の1，0，－1は角運動量のz成分がそれぞれħ，0，－ħであることを表す。

　水素原子には，上記のn＝1，2のエネルギー準位のほかに，n＝3，4，5，……のエネルギー準位がある。主量子数nの準位においては，角運動量量子数lのとりうる値はl＝0，1，2，……，n－1のn個であり，角運動量のz成分を表す量子数（mで表す）のとりうる値はm＝l，l－1，l－2，……，－lの2l＋1個である。ゆえに主量子数nのエネルギー準位には合計n²個の状態がある。このように複数個の状態が等しいエネルギーをもつとき，そのエネルギー準位は縮退しているという。z方向に磁場をかけると，上記の量子数mのそれぞれの値に応じてエネルギーの差ができるので，mを磁気量子数と呼ぶ。

　水素原子がエネルギーの高い定常状態からエネルギーの低い定常状態に遷移すると光を放出するが，量子力学で求められた定常状態のエネルギー準位は，ボーアの原子模型におけるエネルギー準位と一致しているから，放出される光の振動数も同じになり，それはすでに述べたように水素の原子スペクトルの測定結果と一致する。なお，厳密には水素原子は一つの定常状態から他の定常状態に不連続的に飛び移るのではなく，短い時間の間に波動関数が連続的に変化するのであるが，そのような事柄の理解にはかなりの専門的知識が必要である。

　ボーアの原子模型においては電子は円軌道を描いて運動しているが，量子力学においては電子の状態は波動関数で表される。この二つははなはだかけ離れた理論であるが，両者は同じエネルギー準位を与える点では対応関係がある。また，エネルギーの高い状態では電子が陽子から遠くにあるという共通点もある。このような両者の類似点に着目して，1s，2s，2pなどの状態の波動関数を原子軌道関数と呼ぶことが多い。また，さらに省略して単に軌道と呼ぶこともある。

一般の原子

一般の原子では複数個の電子が存在し，電子は原子核から力を受けるだけでなく，他の電子からも力を受けるので，厳密な量子力学的取扱いは困難となるが，概略においては，おのおのの電子が雲のように広がっていて，それらが重なりあって存在していると考えてよい。各電子は原子核の点電荷と，他の電子の雲の電荷とがつくる電場の中に存在することになるが，他電子の雲の電荷は全体としてほぼ球状に分布していると考えてさしつかえない。原子核の点電荷と，そのまわりにある他電子の球状の電荷とのつくる電場の中に電子が存在する場合の個々の電子の波動関数は，水素原子の波動関数と類似したものになり，水素原子の場合と同様に，主量子数n，角運動量量子数l，磁気量子数mをもつ原子軌道関数とその軌道に入っている電子のエネルギー（その軌道関数で表される状態の電子のエネルギー）とが定まる。

　水素原子においては主量子数nの等しい軌道の電子のエネルギーは等しいが，一般の原子の場合は，原子核の外に球状の負電荷があるので少し事情が違っている。角運動量の大きい電子には遠心力が働いて，電子が原子核の近くに存在する確率が小さいので，原子核からの引力は球状負電荷によって比較的に大きな割合で遮られ，結局，電子のエネルギーが高くなる。したがって，例えば，2p軌道に入っている電子のエネルギーは2s軌道に入っている電子のエネルギーよりも少し高い。また，3d軌道の電子のエネルギーは4s軌道の電子のエネルギーよりも高い。エネルギーの低い軌道から順に並べると1s，2s，2p，3s，3p，4s，3d，……となる。

　上述のように，それぞれのn，lの組に対して電子のエネルギーが定まるが，このほかに磁気量子数mがあり，mはl，l－1，……，－lの2l＋1個の値をとるが，これらの2l＋1個の軌道については電子のエネルギーが等しい。前に述べたように，古典力学と量子力学とは必ずしもよく対応しないが，エネルギーが磁気量子数mによらないことは，古典力学的には次のように説明される。すなわち，mは角運動量がz軸に対してどれだけ傾いているかを表す量子数であり，球対称な電場の中ではエネルギーは角運動量の方向には無関係であるから，mの値が異なってもn，lが等しければエネルギーは等しいことになる。

　それぞれのn，l，mに対して一つの軌道が定まるが，パウリの原理によると，一つの軌道に2個までの電子が入ることができ，それより多くの電子が入ることはできない。電子にはスピンがあり，スピンとは自転のことで，電子には二つの自転状態（スピン状態）があるために，同一軌道に2個の電子が入ることができるのである。原子の基底状態においては，エネルギーの低い軌道から順に2個ずつの電子が入っている。1組のn，lに対して，mの異なる2l＋1個の軌道があり，その一つ一つに2個ずつの電子が入りうるから，合計2（2l＋1）個の電子を収容できる。したがって，ns軌道には2個，np軌道には6個，nd軌道には10個，……の電子が入れることになる。エネルギーの低い軌道から順に電子を入れていくと，例えば，酸素原子については1s²2s²2p⁴という電子配置が得られる。ただし，1s，2s，2pの右肩につけた数字は電子の個数を表す。原子番号10までの原子の基底状態の電子配置を列記すると，水素：1s，ヘリウム：1s²，リチウム：1s²2s，ベリリウム：1s²2s²，ホウ素：1s²2s²2p，炭素：1s²2s²2p²，窒素：1s²2s²2p³，酸素：1s²2s²2p⁴，フッ素：1s²2s²2p⁵，ネオン：1s²2s²2p⁶となる。その先の原子については，例えばイオウ：1s²2s²2p⁶3s²3p⁴，塩素：1s²2s²2p⁶3s²3p⁵となる。このような電子配置において，1s²，2s²，2p⁶のように1組のn，lのすべての軌道に電子が2個ずつ入って満員になっている場合には，それを閉殻と呼ぶ。一般に，概略において，主量子数の小さい軌道は原子の内側にあり，主量子数の大きい軌道は原子の外側部分にある。ゆえに，原子は主量子数の順に内から外に配置されたいくつかの殻からなると考えることができ，n＝1，2，3，……に対応してそれぞれK殻，L殻，M殻 ……と呼ぶ。化学反応に関与するのはいちばん外側の殻で，これは外殻と呼ばれ，それ以外の殻は内殻と呼ばれる。例えば，イオウ，塩素などでは1s，2s，2pが内殻であり，3s，3pが外殻である。Li～Neにおいては1sが内殻で，2s，2pが外殻になる。周期表で同族に属する元素の原子が化学的に類似した性質をもつのは，この外殻構造が似ているためで，例えば酸素原子の外殻の電子配置は2s²2p⁴であり，同族のイオウ原子は3s²3p⁴となっている。
→原子核
執筆者：伊藤 敬

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

原子
げんし
atom

通常の化学的な方法ではそれ以上分割できない物質の基本的な構成単位粒子。電気的には中性である。原子の語源はギリシア語で「分割できない」という意味のアトモス（ατομοζ）であるといわれる。実際には、原子は正の電荷をもつ一つの原子核と、その正電荷を打ち消すだけの数の電子から構成され、さらに原子核はいくつかの陽子と中性子からなる。中性子は電荷をもたないために原子核の電荷は陽子によるものである。そのため原子は、これ以上分割できない粒子ではすでにない。しかし、原子をそれ以上に分割すると化学的な性質を失うので、化学的性質を維持するという点では最小の構成粒子である。自然界の物質を構成するもっとも基本的な構成要素は素粒子とよばれ、それはまさにそれ以上に分割できないものと考えてよい。原子の大きさ（直径）はおよそ10^-10メートル（1Å。Åはオングストローム）であるが、原子核の大きさは10^-14メートル程度と非常に小さい。つまり、原子核を直径約7センチメートルの野球ボールとすれば、原子は約700メートルにあたり、野球場全体が優に入るほどの大きさとなる。一方、原子核の質量は電子の質量に比べて非常に大きい。たとえば、水素原子の原子核は陽子1個だけからなり、その質量は約1.67×10^-27キログラムであるが、電子の質量はその1836分の1にすぎない。

［酒井康弘　2017年8月21日］

原子と元素

原子に似たことばに元素があるが、元素は概念であり、同じ化学的性質をもつ原子の総称である。原子の化学的性質は、ほとんどその原子の電子数すなわち陽子の数により定まるので、化学で用いられる周期表は、陽子の数（すなわち電子の数）を示す原子番号によって整理されている。同じ原子番号をもつ原子でも中性子の数が異なるものが存在し、それらはアイソトープ（同位体）とよばれる。これらの総称が元素ということになる。たとえば、元素としての水素には中性子の数が0、1、2個のものが自然界に存在し、それぞれ水素（軽水素、プロチウムともいわれる）、重水素（ジュウテリウム）、三重水素（トリチウム）とよばれるが、それぞれの化学的性質は同じである。

　自然界には、原子番号1番の水素Hから92番のウランUまでの92種の元素が存在するといわれている。ただし、テクネチウムTc（43番）、プロメチウムPm（61番）、アスタチンAt（85番）、フランシウムFr（87番）の4種は、自然界の存在量がきわめて少ない。原子核反応により人工的につくられる元素（超ウラン元素）としては、2016年末の時点で原子番号118までが合成され、それらの名前と記号が国際純正・応用化学連合（IUPAC：International Union of Pure and Applied Chemistry）によって正式に認められている。

　このうち113番元素は、日本の理化学研究所（理研）仁科(にしな)加速器研究センター超重元素研究グループの森田浩介（1957―　）らの実験グループにより、2004年（平成16）に初めて合成され発見されたものである。その後2012年に3個目の合成に成功したことを受けて、2015年12月にそれが新元素であると認定され、命名権を獲得した。2016年11月末に提案通りの元素名ニホニウムnihonium、元素記号Nhが正式に認められた。これまでに、欧米以外の国で元素を発見したグループはなく、日本発の新元素の正式な認定と命名はアジア初である。化学史をひもとくと、今回の新元素発見のはるか昔、1908年（明治41）に東北大学の小川正孝(まさたか)（1865―1930）が原子番号43番の元素を発見したと発表し、ニッポニウムnipponiumと名づけたことがある。しかし、のちにこの発見は取り消され、元素記号として使う予定であった「Np」もネプツニウム（93番）に使われた。また、43番元素は1936年にアメリカの物理学者セグレにより発見され、1947年にテクネチウムと命名された。現在、小川の発見した元素はレニウムRe（75番）であったと考えられている。当時レニウムは未発見の元素であり、小川はその幻の発見者であったといえる。実は、「Np」の記号が与えられたネプツニウムも1940年に理研の仁科芳雄(よしお)により、間接的にではあるがみいだされており（単離できなかったことで発見が認められなかった）、仁科の名前を冠した理研の実験チームによってニホニウムが発見されたことは、奇妙な縁といえよう。

［酒井康弘　2017年8月21日］

質量数と原子量

陽子の数と中性子の数の和は質量数とよばれる。したがって前述のアイソトープ（同位体）は、同じ原子番号でも質量数の異なるものともいえる。同じ質量数で原子番号の異なるものはアイソバー（同重体）とよばれる。質量数は、それを示す必要があるときには¹Hのように添え字で表され、原子番号も併記するときには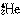のように書かれる。質量数は、統一原子質量単位で表した原子の質量と近似的に等しい。統一原子質量単位は、質量数が12である炭素同位体¹²Cの原子質量の12分の1と定義され、単位はユニット（u）である。周期表中の各元素に原子番号とともに書かれている原子量は、元素の平均的な質量を表す指標である。天然に存在する元素は質量数の異なる数種の同位体の混合物であることから、原子量はその同位体の質量数と存在比をかけて和をとった数として表したものであり、かならずしも整数値とはならない。また、原子量に単位はない。たとえば、天然に存在する炭素には質量数12のものと13および14のものがある。それぞれの同位体存在比は、¹²C（98.9％）、¹³C（1.1％）、¹⁴C（0.0％）であるので、炭素の原子量は、
　　12×0.989＋13×0.011＋14×0.000＝12.011
となる。

［酒井康弘　2017年8月21日］

原子の構造

原子内の電子は原子核の周りを飛び回っているとしてよい。負の電荷をもつ電子が、正の電荷をもつ原子核の周りを両者の間に働く静電的な引力によって軌道運動を行うことは、太陽系における惑星の運動をイメージさせるが、電子が荷電粒子であるという点が異なる。太陽と惑星の場合、両者は互いの引力によって引き合うが、それはつまり太陽の方向に加速度をもつということに対応する。そのままでは惑星は太陽に引き込まれてしまうが、惑星は太陽の周りを回転することで生じた遠心力によって軌道半径を維持できる。原子核の周りを電子が回転するということは、同様の現象のように思える。しかし、イギリスの物理学者マクスウェルの電磁気学によると、加速度運動する荷電粒子は、電磁波を放射し刻々と運動エネルギーを失っていくので、原子核の方向に引き寄せられることになり、軌道半径が縮まっていく。その結果きわめて短い時間（およそ10^-11秒）で原子がつぶれてしまうことになる。もちろん、そのような事実はなく、ある一定の大きさで原子は安定に存在するので、古典物理学の理論ではこの矛盾を説明できない。

　また、惑星の運動と異なり原子内の電子はどんな軌道でも許されているというわけではなく、原子の種類によって決まるとびとびの運動状態（離散的定常状態）しかとりえないことが知られている。これを量子化といい、原子内の電子が量子化されて離散的定常状態をとっていることを原子の電子構造または電子状態とよぶ。また、そのエネルギーはエネルギー準位とよばれる。なぜ、原子内の電子のエネルギーが量子化されているのかもまた古典物理学では説明できず、原子のような小さな世界を記述するには量子力学が必要である。

［酒井康弘　2017年8月21日］

量子力学の骨組み

20世紀初頭ラザフォードにより原子核の存在が確証され原子モデルが提唱されてまもなく、ボーアは、原子内の電子軌道として特定の角運動量をもつものだけが許されるという量子条件を仮定することにより、古典力学とエネルギー量子の考えを折衷した理論（古典量子論）を提唱し、原子スペクトルに関する多くの現象を説明するのに成功した。しかしながら、微視的世界の力学を統一的に理解するためには、アインシュタインとド・ブローイによる物質波の概念やボルンによる波動関数の解釈などを経て、1925年ハイゼンベルクとシュレーディンガーによりそれぞれ独立に建設された量子力学の出現を待たなければならなかった。

　光は電磁波の一種であるが、光電効果の場合のように物質と相互作用する際、量子的なふるまいをする。また電子のような微視的粒子は、電子線回折にみられるように波動性をあわせもっている。このように、微視的物質はすべて粒子と波動の二重性をもつことが20世紀になって知られるようになった。量子力学では古典力学とは対照的に、原子内の電子の状態は波動関数（状態関数）をもって表され、エネルギーや運動量などの力学的量は波動関数に作用する演算子で表される。これらの量の間の関係は基礎方程式であるシュレーディンガーの波動方程式により表される。エネルギーその他の物理量のとりうる値は、波動方程式に適当な境界条件を課したときに、方程式の固有値として求められる。個々のエネルギー固有値に対応する波動関数の解は固有関数とよばれる。空間の各点で電子がみいだされる確率は波動関数の2乗で与えられる。

　このように、電子がある時刻にどの場所にいるかということは量子力学では一意的に定まらず、確率が定まるだけである。したがって原子内の電子の運動状態を表すのに古典力学のように決まった軌道を考えるのは間違いで、状態関数の2乗で表した電子雲のような描像を描くのが適切である。その雲の濃淡が、その場所に電子がみいだされる確率の大きさを示すのである。量子力学によれば、原子がとりうる定常状態のエネルギーの値や、原子が光を吸収したり放射したりしてエネルギー準位の間でおこす遷移のおこりやすさなどを一貫した理論体系のなかで正確に計算することができる。

［鈴木　洋］

原子の電子殻構造

原子内の電子の定常状態を指定するのに普通4個の量子数の組を使う。主量子数nによりエネルギーのだいたいの大きさが定まる。エネルギーがもっとも低い（束縛エネルギーが大きい）ほうから高いほうへn＝1, 2, 3,……の順になっている。方位量子数lは電子の角運動量の大きさを表し、普通l＝0, 1, 2, 3,……に対応して固有状態をs, p, d, fの記号で表す。一つの角運動量をもつ状態はさらに磁気量子数m_l（角運動量のz成分を表す量子数）で区別される。決まったlの状態に対して許されるm_lの値は
　－l,－l＋1,……, 0,……, l－1, l
の2l＋1個である。すなわち、磁場をかけるとこれだけの数の状態に分離する。最後にスピン量子数m_sは＋1/2か－1/2をとる。

　原子内電子は、基底状態ではエネルギーの低い内側の状態から順に席を占める。ただし、パウリの排他律とよばれる法則があって、一つの量子状態を1個以上の電子が占めることはできない。このため原子内の電子は、その数が増えるにしたがってエネルギーの低い内側の軌道から順に詰められていく。各軌道の収容能力は、1sに2個（スピン＋1/2と－1/2）、2sに2個、2pに6個（l＝1の軌道は磁気量子数の違いにより3個の準位に分かれる）、3sに2個、3pに6個、3dに10個（l＝2の軌道は磁気量子数の違いにより5個の準位に分かれる）というように定まっている。主量子数の等しい状態はエネルギーについてひとまとめとして扱えるので、同一の電子殻に分類される。nが1、2、3、4、5の殻をそれぞれK、L、M、N、O殻とよぶ。各殻に含まれる状態数は、K殻に2個、L殻に8個、M殻に18個となる。

［鈴木　洋］

原子の電子殻構造と化学的性質

以上のような殻構造を念頭に置くと、元素の種々の化学的性質が周期律に従って変化することが、よく理解できる。希ガス元素ヘリウムHe、ネオンNe、アルゴンArなどでは、それぞれK殻、L殻およびMの副殻（3p軌道まで）に電子がちょうどいっぱいに詰まっており、そのため化学的にもっとも不活性である。アルカリ金属リチウムLi、ナトリウムNa、カリウムKなどでは閉殻の外の殻に1個だけs電子があるので、イオン化エネルギー（電子を1個取り去るのに必要なエネルギー）がとりわけ小さく、他の原子に電子を与えて正イオンになりやすい性質をもっている。一方、ハロゲン族フッ素F、塩素Cl、臭素Brなどでは、希ガス原子のように閉殻をつくるには電子が1個足りないので、電子をもらって1価の負イオンになりやすい性質をもつ。

　普通、ある元素の原子1個が特定の原子（水素原子を標準にとり1とする）何個と結合するかを示す数を原子価とよび、原子間に結合が形成される機構を考える基本となるが、原子価は、原子の最外殻にあって化学反応に参加する電子（価電子）の数によって決まる。

［鈴木　洋］

原子内電子の束縛エネルギー

ウランやプルトニウムを使った原子炉から取り出されるエネルギーを一般に原子エネルギーとよぶ習慣があるが、これは誤解を伴いやすい。原子炉のエネルギーは原子核分裂により発生するものであり、原子核エネルギーとよぶのが正しい。原子のエネルギーはむしろ化学反応のエネルギーに近い。

　原子のいちばん外側にある電子を原子の外に取り去るのに要するエネルギーは最小イオン化エネルギーとよばれる。いちばん大きな値をもつものはヘリウムで24.58電子ボルト、いちばん小さい値はセシウムの3.9電子ボルトである。ここで電子ボルトは、素電荷をもつ粒子が1ボルトの電位差で加速されるとき獲得するエネルギーで、約1.6×10^-19ジュールに相当する。

　原子内電子のうちいちばん大きなエネルギーで束縛されているのは最内殻（K殻）の電子である。天然元素ではウランのK殻電子のエネルギーが最大で、この値は約11万6000電子ボルトである。このような内殻準位のエネルギーに関する知識は、元素の特性X線やX線光電子スペクトルの測定から得られる。

［鈴木　洋］

『『量子力学的世界像』（『朝永振一郎著作集8』1982・みすず書房）』▽『エミリオ・セグレ著、久保亮五・矢崎裕二訳『X線からクォークまで――20世紀の物理学者たち』（1982・みすず書房）』▽『G・ヘルツベルク著、堀健夫訳『原子スペクトルと原子構造』（1988・丸善）』▽『長島順清著『素粒子物理学の基礎1』（1998・朝倉書店）』▽『荒船次郎・江沢洋・中村孔一・米沢富美子編、高柳和夫著『原子分子物理学』（2000・朝倉書店）』▽『高田健次郎著『わかりやすい量子力学入門――原子の世界の謎を解く』（2003・丸善）』▽『吉原賢二「小川正孝のニッポニウム研究について」（『化学と工業』Vol.66, No.7, pp.538～540・2013・日本化学会）』▽『ジャン・ペラン著、玉虫文一訳『原子』（岩波文庫）』

[参照項目] | アイソトープ | イオン | エネルギー準位 | 殻構造 | 核分裂 | 原子核 | 元素 | 元素記号 | 質量数 | 周期表 | 素粒子 | 中性子 | 電子 | ニホニウム | 陽子 | 量子力学

原子の構成要素

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

原子
げんし
atom

荷電粒子を発生させることなく分割できる物質の最小単位。これはまた元素に特有な性質を維持できる物質の最小単位でもある。原子の概念は紀元前5世紀のギリシアの哲学者デモクリトスの唱えた「アトモス」 (「不可分な」の意) に始る。この見解は長く支配的で，19世紀に入って近代的な科学実験と数学的な演繹による物質の構築単位に関するさらに精密な概念が生じるまで続いた。 1808年イギリスの化学者 J.ドールトンにより統一的な原子論が提唱された。原子そのものの研究に基づく近代原子論の基礎となったのは，E.ラザフォードによる原子構造の解析と，H.G.J.モーズリーによる原子番号のもつ物理的意義の解明である。これにより原子は原子核と核外電子から成ることが確かめられた。
すべての物質は分子の集りから成る。さらに，分子は化学結合によって結ばれた原子から成る。個々の原子は電子と原子核から構成される。原子もまた大きなエネルギーを加えることによってその構成粒子に分けられる。原子核を構成する陽子と中性子および電子もさらに巨大なエネルギーを与えると，寿命の短い各種の素粒子に分けることができる。原子の中央に陽子と中性子から成る稠密な中心部である核がある。これらの核子は小さいが非常に重く，核は原子全体の質量の 99.9%以上を構成するが，体積はおよそ 10^-14 を占めるだけである。核子はきわめて近接したときに核力が働き，互いに結着して核を形成する。陽子はそれぞれ正の電荷をもち，中性子はまったく電荷をもたないため，核は正の電荷を帯びている。陽子と中性子はどちらも小さな粒子であるが，これらはクォークと呼ばれるさらに小さな粒子により構成されている。核のまわりは，負の電荷をもち質量がほとんどない電子という粒子の拡散した雲でおおわれている。相反する電荷同士は引きつけ合うので，負に荷電した電子は正に荷電した核に拘束される。電気的に中性の原子の中では，電子の数は核の正電荷数 (つまり核中の陽子数) と等しい。
しかし原子は全体として，正の電荷よりも多かったり少かったりする電子をもつこともある。こうした荷電原子はイオンと呼ばれる。各原子あるいは各イオンの内部では，電子は静止しているのではなく核の周囲をめぐる複雑な軌道上を動いていると考えられる。1つの原子の大きさ，他の原子や粒子および電磁放射に対する反応性は，核の周囲をまわっている電子の配置で決定される。原子は電子の転移や共有を行うことで互いに結合して，分子のようなより大きな構造を形成する (→原子価電子 ) 。1つの原子核に結びついている電子が近くの他の原子核と引きつけ合う現象 (→ファン・デル・ワールス力 ) によって，液体や固体の形成機構をほぼ説明できる。原子の最も重要な特性は核内にある陽子の数を示す原子番号である。同じ原子番号の原子はすべてほぼ同一の化学的特性をもち同族の元素を構成する。元素を構成する原子がすべて核内に同じ数の中性子をもっているわけではない。原子番号が同じでも中性子の数が異なる原子を，その元素のアイソトープと呼ぶ。アイソトープは同じ化学的特性をもちながらも，質量，核反応における放射性の傾向，磁気特性といった異なる核の特性を示す。原子に関する研究は水素原子のスペクトルの解析，アイソトープの発見，量子力学の導入，素粒子の発見などにより補足され，精密化され，現在にいたっている。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

原子

原子は物質要素の実体を指す呼び名で、「これ以上分けることができないもの」という意味。元素は同種の原子を包括する呼び名。原子の種類は全宇宙を調べても92種類ほどしかなく、人工的に作られた元素を含めて113種が知られている。自然界の多様性、人工的に作り出された様々な物質のすべては、これらの原子の組み合わせからできている。原子に内部構造があることを最初に実験的に示したのは、トムソン(J.J.Thomson、1856〜1940)で、負(-)の電荷を持った軽い粒子(電子)がすべての原子の中に存在することを明らかにした。ラザフォード(E.Rutherford、1871〜1937)は原子の中に正(+)の電荷を持つ成分として、大きさが10兆分の1cm程度の、原子の大きさより5桁も小さい重い粒子(原子核)の存在を明らかにした。原子核は正の電荷を持つ陽子と、電荷を持たない中性子からできており、陽子と中性子の質量はほぼ等しく、電子の質量の1840倍あり、原子の質量の大部分を占めている。原子核の中にある陽子の数(Z)が原子の種類を決め、Zの値が原子番号となる。原子は全体として電気的に中性で、電子数は陽子数と等しく、原子番号により化学的性質がほぼ決まる。原子には、陽子の数Zが等しくて、中性子の数Nが異なる原子があり、それらを互いに同位体(アイソトープ)という。陽子の数(Z)と中性子の数(N)の和A(=Z+N)が質量数で、同位体を区別している。自然界で不変の安定同位体と一定の半減期を持ち、放射線を出して崩壊する放射性同位体がある。質量数12の炭素原子が約6.02×10^23個(アボガドロ定数と呼び、物質量1モルという)集まると質量12gになる。元素の周期表に書かれている原子量は、質量数12の炭素の原子量を正確に12と決め、各元素の安定同位体の存在比をかけて加重平均を取り、相対的な質量として示してある。物質の組成として、1種類の原子しか含まれない場合を単体といい、同種の原子からできた単体で構造も性質も異なるものを同素体と呼ぶ。酸素分子とオゾンがその例。一方、2種類以上の原子からできている分子を化合物という。単体や化合物が、それぞれ、目に見えるくらい多量に集まった集合体は純物質で、2種類以上の純物質の集まりを混合物という。

(市村禎二郎 東京工業大学教授 ／ 2007年)

原子

原子核とマイナスの電荷をもつ電子からなる粒子。原子核はさらにプラスの電荷をもつ陽子と電荷のない中性子で構成される(ただし、大部分の水素原子は中性子をもたない)。陽子の数を原子番号、陽子と中性子の合計数を質量数と呼ぶ。同じ原子でも中性子の個数が違うものがあり、同位体という。どの原子のどういう同位体かを示すのが核種。例えば炭素原子は「炭素12」「炭素13」「炭素14」の3つの核種が存在する。原子名のあとの数字は質量数。原子はふつう陽子の数と電子の数が等しいので電気的には中性である。しかし、電子が何個かはがれたり、付け加わったりすると全体としてプラスやマイナスの電荷をもつようになる。この状態をイオンと呼ぶ。原子が化学結合によって複数結びつくと分子となる。

(渥美好司 朝日新聞記者 ／ 2008年)

出典　(株)朝日新聞出版発行「知恵蔵」

化学辞典 第2版

原子
ゲンシ
atom

物質を形づくっている最小単位．原子核とその電荷と同数の電子との組合せでできている．原子核の電荷数が1である水素原子Hからはじまり，電荷数111のレントゲニウムRgまで知られている．これらの原子の種々の結合により分子ができている．J. Dalton(ドルトン)が原子論を唱えたときは，物質の性質をもつ最小単位を原子とよんだが，その後，定比例の法則，倍数比例の法則などの発見によって，Daltonのいう原子は分子であり，分子はいくつかの原子の結合によってできているとするほうがよいことが明らかになった．現在では，原子核を構成しているのは陽子と中性子であることが知られているが，原子核の電荷数は陽子の個数に等しく，中性子の数には自由度がある．原子の化学的性質は，おもに原子核のまわりの電子数によって決まるので，陽子数が同じで中性子数が違う原子は，化学的性質はほとんど同じであり，同位体とよばれる．原子核中の中性子数は，陽子の数に対し，ある限られた数のときに安定なので，その関係からはずれるような原子核は自然に崩壊する．このような同位体は放射性同位体とよばれる．希ガスのように原子が1個で安定な単原子分子となるものもいくつかあるが，一般には原子が単独のときは反応性が高く，ほかの原子と結合して分子となってはじめて安定であるもののほうが多い．原子をつくり出すには，放電や短波長の光照射などがよく用いられる．金属などでは真空中で高温に熱するだけで原子が飛び出してくるものも多い．

出典　森北出版「化学辞典（第2版）」

百科事典マイペディア

原子【げんし】

物質を構成する基本的要素の一つで，原子核と電子からなる。いずれも直径10(-/)⁸cm程度の粒子で，水素原子が最小。すべての物質は原子から生じたイオン，あるいは原子が組み合わさってできた分子からなりたつ。物質を構成する究極の単位としてギリシア語atomos（分割できないもの）にちなんでatomと命名された。→原子構造／原子論
→関連項目モル

出典　株式会社平凡社

世界大百科事典（旧版）内の原子の言及

【原子論】より

…物質を分割していくと，それ以上分割できない究極･最小の単位すなわち〈原子〉に到達する，という説を原子論の定義として採るとすれば，後述されるように古代インドにも原子論は認められる。しかし以下のような，ギリシア＝ヨーロッパの原子論(アトミズム)の伝統のもつもう一つの論理的特徴はもたないと考えられる。…

【周期律】より

…元素の物理･化学的性質は，その原子番号の増加とともに周期的な変化をくりかえしていくという化学の根本的な法則。これを表の形で表したものが周期表である。…

【素粒子】より

…19世紀になって，イギリスの化学者J.ドルトンは，このような物質の最小の単位の存在を科学的に証明し，これに古代ギリシアの〈アトム〉という名を与えた。これが原子である。原子は確かに物質を構成する基本粒子であり，化学的性質を保つ最小の単位ではあったが，しかし20世紀に入ると，この原子はそれ自身決して分割不可能なものでなく，中心に原子核という小さな粒子があって，そのまわりをいくつかの電子という小さな粒子が回っていることが明らかにされ，さらに原子核も陽子と中性子の複合体であることがわかった。…

※「原子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」