精選版 日本国語大辞典 「ボルツマン定数」の意味・読み・例文・類語
ボルツマン‐ていすう【ボルツマン定数】
日本大百科全書(ニッポニカ) 「ボルツマン定数」の意味・わかりやすい解説
ボルツマン定数
ぼるつまんていすう
Boltzmann constant
オーストリアの物理学者ボルツマンの導入した普遍定数の一つ。理想気体1モルの圧力をp、体積をV、絶対温度をTとすると、これらの間には状態方程式pV=RTが成り立つ。比例定数Rは気体定数とよばれるが、これをアボガドロ数(モル分子数)NAで割ったもの
k=R/NA=1.380658×10-23J・K-1
をボルツマン定数という。気体分子の重心運動のエネルギーは
と書かれるが、多数の分子(または1個の分子の長時間)についての平均値(〈 〉で示す)は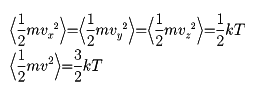
となることが知られている。もっと一般に、固体や液体内の原子の不規則な運動についても同じ関係が成り立つ。したがってkTという量は、温度Tの系内の微視的な運動のエネルギーのだいたいの程度を示す量であると考えることができる。このため、kTは統計分布の式(フェルミ‐ディラック統計、ボース‐アインシュタイン統計、マクスウェル‐ボルツマン統計)において重要な役割を果たす。また、ボルツマンの墓に刻まれているので有名な、エントロピーの式S=klogWにもボルツマン定数が出てくる。
[小出昭一郎]
改訂新版 世界大百科事典 「ボルツマン定数」の意味・わかりやすい解説
ボルツマン定数 (ボルツマンていすう)
Boltzmann's constant
普遍定数の一つ。気体定数Rをアボガドロ数NAで割ったもの。ふつうkで表され,その値はk=R/NA=1.38066×10⁻23J・K⁻1。ボルツマン定数は統計力学におけるもっとも基本的な定数であるが,裏話をすると,単に歴史的なりゆきのため,温度を定義する際に,エネルギーの単位で測ればよいのに,エネルギーをkで割ったものを単位にしてしまったことが,kの存在を必要不可欠にしてしまったといえる。1気圧での氷の融点と水の沸点の温度差を100℃とするなどということは,人間の恣意(しい)にすぎない。
物理学の論理のうえでは,エントロピーSは,ボルツマンの原理により,状態数をWとして,
S=klogeW
で定義される。これによれば,内部エネルギーをUとして,
∂S/∂U=1/T
が温度Tの定義となる(微分の際に体積Vは一定にする)。簡単にいうと,熱量⊿Qを受け取った系のエントロピーは,
⊿S=⊿Q/T
だけ増すとされ,これが絶対温度の定義になっていた。論理のむだを省くには,エントロピーの定義を,
S=logeW
とし,
∂S/∂U=1/T′
で定義されるT′を温度と名づければよかったのである(T′=kT)。実際問題として,カノニカル分布,フェルミ=ディラック分布,ボース=アインシュタイン分布,マクスウェル=ボルツマン分布など,統計力学の基本的公式の中に表れる温度は必ずボルツマン定数を伴ったkTの形で現れる。
執筆者:伊豆山 健夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「ボルツマン定数」の意味・わかりやすい解説
ボルツマン定数
ボルツマンていすう
Boltzmann constant
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「ボルツマン定数」の意味・わかりやすい解説
ボルツマン定数【ボルツマンていすう】
→関連項目気体定数|熱中性子|普遍定数
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「ボルツマン定数」の解説
ボルツマン定数
ボルツマンテイスウ
Boltzmann constant
気体定数(R)をアボガドロ定数(NA)で割った数.記号k.
k = R/NA
基本物理定数の一つ.もっとも新しい数値は
k = 1.380503(24)×10-23 J K-1
物理学および物理化学の理論によく用いられる.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
法則の辞典 「ボルツマン定数」の解説
ボルツマン定数【Boltzmann constant】
世界大百科事典(旧版)内のボルツマン定数の言及
【温度】より
…希薄な気体の場合,個々の分子はいろいろな速度,したがって運動エネルギーで運動しているが,ある一つの分子がエネルギーEをもつ確率は,気体の温度をT(K)とすると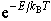 に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10-23J・K-1に等しい。統計力学によると,一般に巨視的な物体においてエネルギーは気体のときと同様にそれを構成する非常に多くの粒子(正確には力学的自由度)に乱雑なしかたで分配されている。…
に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10-23J・K-1に等しい。統計力学によると,一般に巨視的な物体においてエネルギーは気体のときと同様にそれを構成する非常に多くの粒子(正確には力学的自由度)に乱雑なしかたで分配されている。…
【気体定数】より
…1molの気体は,1気圧,0℃の状態で22.4lの体積を占めることを利用すると,気体定数はR=8.31J/mol・K=0.082l・atm/mol・Kと計算される。なお,気体定数をモル分子数で割ったものはボルツマン定数である。【阿部 竜蔵】。…
※「ボルツマン定数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...

