ドモアブルの定理（読み）ドモアブルのていり（その他表記）de Moivre’s theorem

改訂新版　世界大百科事典

ド・モアブルの定理 (ドモアブルのていり)
de Moivre’s theorem

nを任意の整数（正でも負でもよいし0でもよい）とするとき，

　（cos θ＋i sin θ）ⁿ＝cos nθ＋isin nθ

が成立する。これをド・モアブルの定理といい，複素数と三角関数とを結ぶ基本定理の一つである。これを用いると任意の複素数aのn乗根（nは自然数），すなわちzⁿ＝aとなるzが次のようにして求められる。a＝0ならばz＝0だからa≠0とすると，a＝r（cosθ＋isin θ）（r＞0）と表される。

　そこで，

　z＝R（cosφ＋isinφ）　（R＞0）　

とおくと，zⁿ＝Rⁿ（cosnφ＋isinnφ）となるから，zⁿ＝aとなるR，φを求めると，

を得る。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ド・モアブルの定理
どもあぶるのていり

複素数zを極形式で表してz=r(cosθ+isinθ)とすると
　　z²=r²(cos2θ+isin2θ)
　　　　………………
　　zⁿ=rⁿ(cosnθ+isinnθ)
となる。とくにr=1のときがド・モアブルの定理である。つまり、
　　(cosθ+isinθ)ⁿ
　　　　=cosnθ+isinnθ
これは、nがゼロ、または負の整数のときにも成り立つ。

［寺田文行］

[参照項目] | 複素数

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

ド・モアブルの定理【ドモアブルのていり】

iを虚数単位，θを任意の実数，nを任意の有理数とするとき（cos θ＋i sin θ）(n/)＝cos nθ＋i sin nθという定理。複素数のべき，べき根の計算等に使われる。→ド・モアブル

出典　株式会社平凡社

世界大百科事典（旧版）内のドモアブルの定理の言及

【三角関数】より

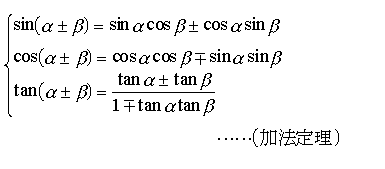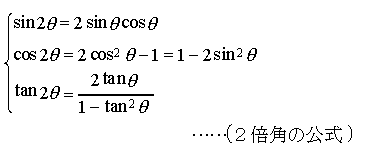
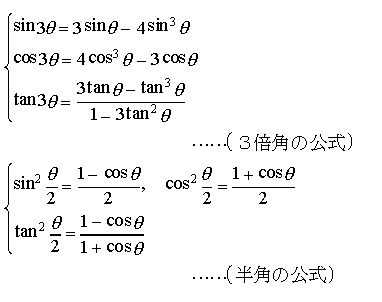
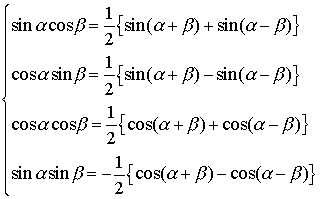
…この加法定理から，次の2倍角の公式，3倍角の公式，半角の公式，正弦･余弦の積を和に変える公式，和を積に変える公式が導かれる。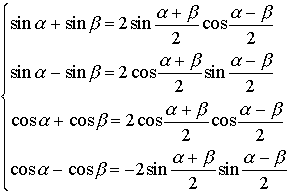次の公式はド･モアブルの定理と呼ばれ，複素数の累乗，累乗根などの計算に使われる。nを正の整数，iを虚数単位とすると，　(cosθ＋isinθ)ⁿ＝cosnθ＋isinnθ
［単振動］
　図3において，OPが一定の角速度ωで回転しているとし，時間t＝0のときθ＝αであったとする。…

【ド･モアブル】より

…これは今日ド･モアブル=ラプラスの定理と呼ばれている。ド･モアブルの定理(公式)と呼ばれる式は，複素数と三角関数を結ぶ基本公式として有名である。【飛田 武幸】。…

【偏角】より

…とくに自然数nについて，　(cosθ＋isinθ)ⁿ＝cos(nθ)＋isin(nθ)となる。これをド･モアブルの定理(公式)という。【斎藤 裕】。…

※「ドモアブルの定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」