フェルミ=ディラック分布（読み）フェルミディラックぶんぷ（その他表記）Fermi-Dirac's distribution

改訂新版　世界大百科事典

フェルミ=ディラック分布 (フェルミディラックぶんぷ)
Fermi-Dirac's distribution

電子や³Heや核子（陽子，中性子）のようなフェルミ粒子それぞれの集団を考える。集団の中で各粒子はほとんどほかとは独立に運動しているとみなしうるとしよう。独立に運動している粒子の量子状態に番号をつけて，1，2，3，……とし，j番目の量子状態のエネルギーをε_jで表すことにする。量子状態jを占めている粒子の数n_jを観測すれば，1回の観測では0または1であるが，粒子集団が絶対温度Tの熱平衡にあれば，粒子数の平均値は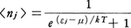，で与えられる。これをフェルミ=ディラック分布，または単にフェルミ分布Fermi distributionという。ここにkはボルツマン定数，μは化学ポテンシャルで，後者は〈n₁〉＋〈n₂〉＋……が粒子の総数に等しくなるという条件で決まる。粒子の総数を固定すれば，μは温度Tの関数となるが，T→0でのμをとくにフェルミ準位という。T＝0ではε_j≦μの場合〈n_j〉＝1で，ε_j＞μでは〈n_j〉＝0となる。これがフェルミ縮退である。
執筆者：伊豆山 健夫

出典　株式会社平凡社「改訂新版　世界大百科事典」